除此之外,我们还可以利用触发器来进行数的运算。下面,我们就来看一下,它是如何实现两个数相加的。
如图所示,把3排触发器按图中的样子连起来。第一排触发器用来记被加数,第二排用来记加数,最后一排记二者加起来的和。当上面的两排触发器的状态为“1”时,会向第三排的触发器输出脉冲信号。
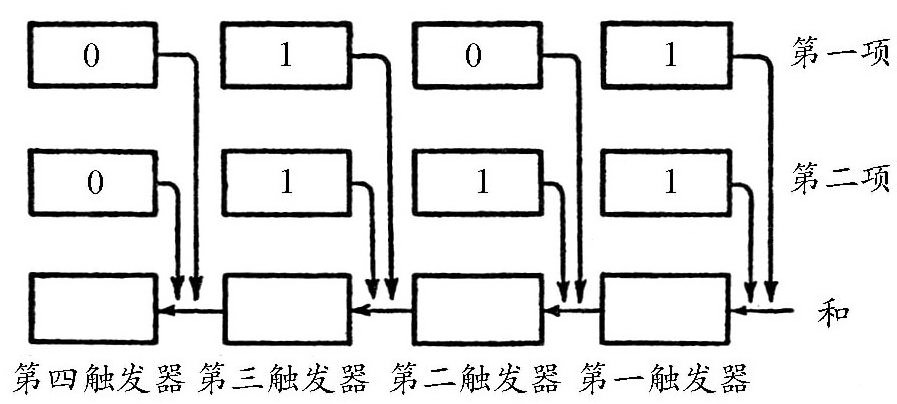
从图中可以看出,上面两排触发器分别记着二进制数101和111。最后一排的第一个触发器从上面两排的第一个触发器各得到一个脉冲信号,即共得到两个脉冲信号。根据前面的分析,此时最下面的第一个触发器仍然处于“0状态”,同时会给第二个触发器发送一个回答脉冲。另外,第二个触发器还会从第二个二进制数那里得到一个脉冲信号。也就是说,这个触发器共得到了两个脉冲信号,因此,该触发器也处于“0状态”,并且,它还会向第三个触发器发送一个回答脉冲。除了得到这个回答脉冲之外,第三个触发器还从上面的两个触发器中得到了两个脉冲。也就是说,该触发器共得到3个信号,结果变成“1状态”,同时输出一个回答脉冲。第四个触发器得到了这个回答脉冲,并且再没有其他脉冲信号输入,因此第四个触发器的状态为“1”。以上的过程实现了两个二进制数的加法运算,即
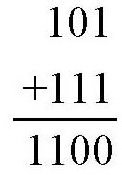
如果换算成十进制的数,就是5+7=12。在图中,最下面一排触发器输出的回答脉冲,就相当于我们在用“竖式”进行加法运算时的进位。如果每排触发器不是4个,而是20个甚至更多,我们就可以进行百万甚至千万级的数的加法运算。
需要指出的是,借助触发器进行加法运算的实际装置,要比图中的情况稍稍复杂。在实际的装置中,我们还需要考虑信号的“延迟”,通过一些装置来实现这一功能。具体地讲,在图中,在接通装置的瞬间,上面两排触发器输出的脉冲同时加在最后一排的第一个触发器上,两个信号很容易混合在一起,被误认为接收到的只有一个信号。为了避免这种现象发生,必须让上面的两个信号分先后到达,即后一个信号要比前一个信号“延迟”到达。如果加上这一延迟装置,两个数相加的时候,就会比触发器单纯计数花费的时间要多一些。
将上面的设计方案稍加改造,就可以进行减法运算,甚至乘法运算、除法运算。事实上,乘法运算就是连续的加法运算,因此,花费的时间就会比加法运算多很多。
以上过程即是现代计算机的计算原理。应用这一装置的计算机每秒可以运算1万甚至10万多次,未来每秒运算速度甚至会达到上百万次、上亿次。读者朋友,你可能会觉得,这么快的运算速度有什么用处呢?在很多人看来,要计算一个15位数的平方,用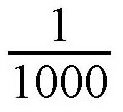
秒的时间来计算跟用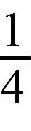
秒的时间来计算,好像没有什么太大的差别,都是一瞬间而已嘛。
其实不然。我们不妨先来看一个例子:一个非常优秀的象棋选手,在下每一步棋的时候,落子之前往往要考虑几十甚至上百种可能的情况。假设他考虑一种情况需要花费几秒,上百个方案就要花费几分钟甚至几十分钟。这样的话,在复杂的棋局中,棋手就会感到时间不够用,因为思考的时间可能会占用整个比赛所规定的绝大部分时间,导致最后只能匆忙落子。但是,如果把分析走棋方案的工作交给计算机来做,会怎么样呢?计算机每秒能进行上万次的运算,它分析完所有的走棋方案只需要一眨眼的工夫,当然不会出现时间不够用的情况。
你可能会说,计算是计算,下棋是下棋,它们是不一样的。棋手下棋的时候,可不是在计算,而是在思索,计算机怎么可能会下棋呢?你无须疑惑,我们在后面的章节中会对这一问题再进行详细的分析。
