在前面的几个章节,我们跟着凡尔纳进行了地心旅游。并了解了气压和深度的关系,对地心有了更科学的认识。现在,我们来想象往天上飞。我们同样可以利用前文中提到的公式,不过它在这里要变一变形:
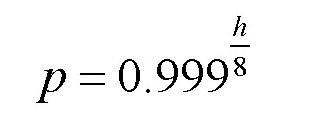
这里的p指的是大气压,h指的是上升高度(单位为米);0.999就是代替1.001的角色(因为高度每上升8米,大气的压力都要减少0.001倍,所以比例关系就变成了原来的0.999倍)。
现在,我们就来解决这样一个问题:想要飞到空气压力只有以前一半的地方,需要飞多高?
根据上述要求,大气压力P等于0.5,代入公式,可以得到下面的算式:
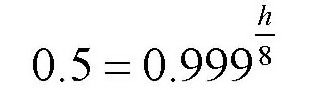
运用对数,我们可以得出h=5.6千米。也就是说,要让大气压力减少一半的话,需要上升到5.6千米的高度。
我们跟着探险家飞到更高的地方——19千米、22千米。这两个高度已经位于我们常说的平流层了。
我们来算一下,这两个高度的大气压是多少。
当高度h=19千米时,大气压力的公式是:

当高度h=22千米时,大气压力的公式是:

上面是通过公式得出的结果,但根据探险家们的记录,在飞到这样的高度时,大气压的大小是另外的数值:
在19千米处时,大气压力是50毫米汞柱。
在22千米处时,大气压力是45毫米汞柱。
为什么结果会不一样呢?错误出在了哪里?
有些读者应该已经想到了——是温度。马里奥特定律适用的前提是:在压力比较小的情况下。刚才的计算和实际结果不相符,就是因为我们疏忽了温度这个因素。我们把整个20千米厚度的大气温度都看成是一样的,认为温度是保持恒定的了。事实上,实际并非如此,随着高度的不断增大,空气温度会随之逐渐减小。一般情况下,每上升1千米的高度,空气温度平均就会下降6.5℃。以此类推,到达11千米的高空时,温度已经下降到零下56℃了。再继续上升的话,温度在很长一段距离之内都不会改变了。如果把温度的因素也考虑进去的话(初等数学在这里已经完全不适用了),我们就能够得到更符合实际情况的答案。同样,因为温度的变化,我们在前面所计算的在地下深处的大气压,也只能用近似值来表示。
1马克·吐温(1835~1910),美国著名作家,演说家,代表作有《汤姆·索亚历险记》《百万英镑》等。
2英国有位物理学家曾计算过,假如地球引力有一天突然消失了,水也就没有了质量,那么被压缩的水就会恢复成原来的体积。这样的话,海平面平均就会上升35米。这时,海水会淹没5000000平方千米的陆地。因为陆地之所以能出现在水面上,就是因为周围的海水被压缩了。
31海里≈1.8千米。
4蒙哥尔费兄弟,法国航空先驱、热空气气球的发明人。
5米哈伊尔·瓦西里耶维奇·罗蒙诺索夫(1711~1765),俄国百科全书式的科学家、语言学者、哲学家和诗人。
6这里之所以不用半球的表面积,而是用圆的面积,是因为只有当大气压力垂直作用于物体表面的时候,上述数据才会成立。作用于斜面上的压力比较小。我们这里用的是大圆的面积,就是一个完整的球的表面投射在平面上的正射影。
7皮埃尔· 西蒙· 拉普拉斯(1749~1827),法国分析学家、概率论学家、物理学家。
