【题目】如图所示,在一条铁路线的一边有一座村庄B,它距离铁路线的距离是20千米。现在要在铁路线上设一座车站C,使得沿铁路AC和沿公路CB,即从点A到点B所用的时间最短。已知火车的速度是0.8千米/分钟,沿着公路行进的速度是0.2千米/分钟。请问,车站C应该设在哪里?
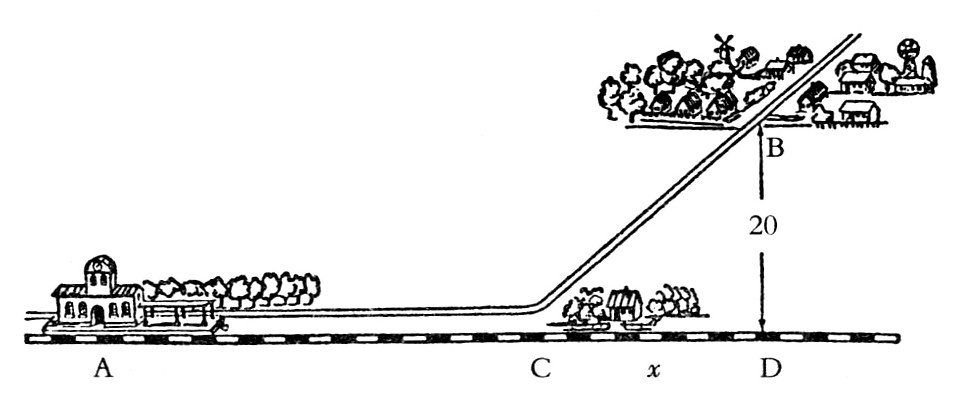
图
【解答】设图中的距离AD为a,距离CD为x,则
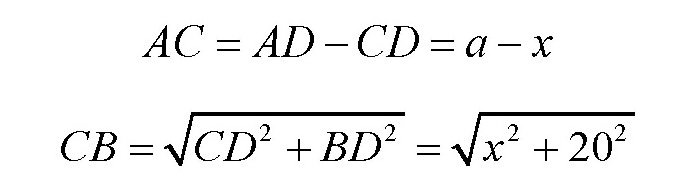
乘坐火车从点A到车站C的时间为
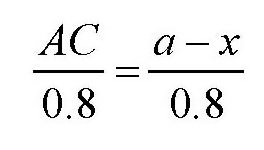
步行从车站C到村庄B的时间为
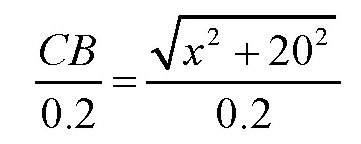
从点A到点B所用的总时间就是

问题即求上式的最小值。
设
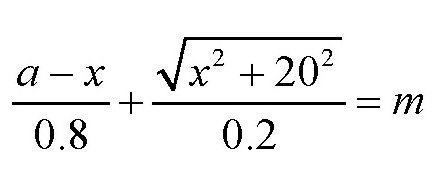
变形后得到
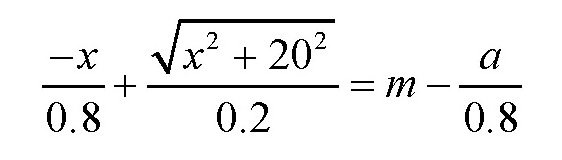
等式两边同乘以0.8,得
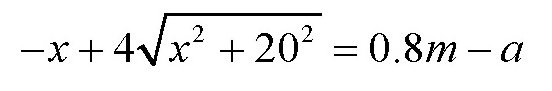
再设k=0.8ma,化简后得到下面的方程
15x2-2kx+6400k2=0
解方程得
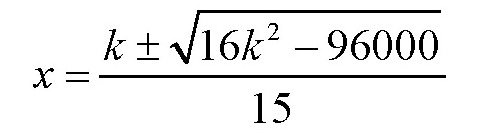
由于k=0.8m-a,所以当m取最小值的时候,k也取最小值,反过来也一样。由于x必须是实数,所以(16k2-96000)应该不小于0。也就是说,16k2的最小值为96000。这时,
16k2=96000
当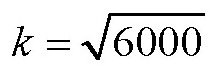
时,m的值最小。此时
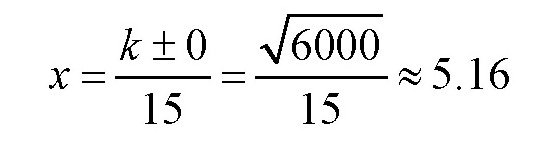
所以,这个车站C应该设在距离点D大约5千米的地方。
在以上的分析过程中,并没有考虑a的大小,在一开始我们就假设a>x,所以只有当a<x时,方程的解才有意义。如果x=a≈5.16,或者当a<5.16千米,那么根本不需要设置车站C,只要沿公路从点A到点B就可以了。
在本题中,我们比方程考虑得更周到一些。如果只是一味地信任方程,就会在x=a的情况下继续在车站A的旁边设一个车站C,这完全是一个笑话。因为在这种情况下,x>a,乘坐火车的时间成了负数。这个题目给读者这样的启示:在利用数学工具解答实际问题的时候,必须非常小心,如果脱离了实际,就会得出令人啼笑皆非的结果。
