当我们站在一望无垠的平原上,经常感觉自己仿佛置身于一个看不到边的圆面中心,地平线就是这个圆面的边缘。而地平线是没有办法触摸到的:如果向它走去,它就会向后退。不过,虽然我们无法接近它,它却是客观存在的。这不是我们视力上的错觉,也不是幻景。
对于地球上的每个观测点,都存在着一条地球表面的界线,我们就是通过这个点看过去的,同时我们还可以计算出这个界线的距离。
如图所示,这是地球的一部分,我们来看一下地平线的几何关系。假设观察者的眼睛在点C,眼睛离地面的高度是CD。如果他向周围看去,那么他能在平地上看到多远的距离?从图上可以看出,他只能看到圆周M、N上的各点,在这个圆周上,他的视线跟地球表面相切,再远的范围就在他的视线之外了。M、N两点以及所有圆周上的各点就是这个人能看见的地球表面的边界。也就是说,就是这些点连成了地平线。在观察者看来,天穹和大地在这里相接,他在这些点上同时看到了天空和地上的物体。
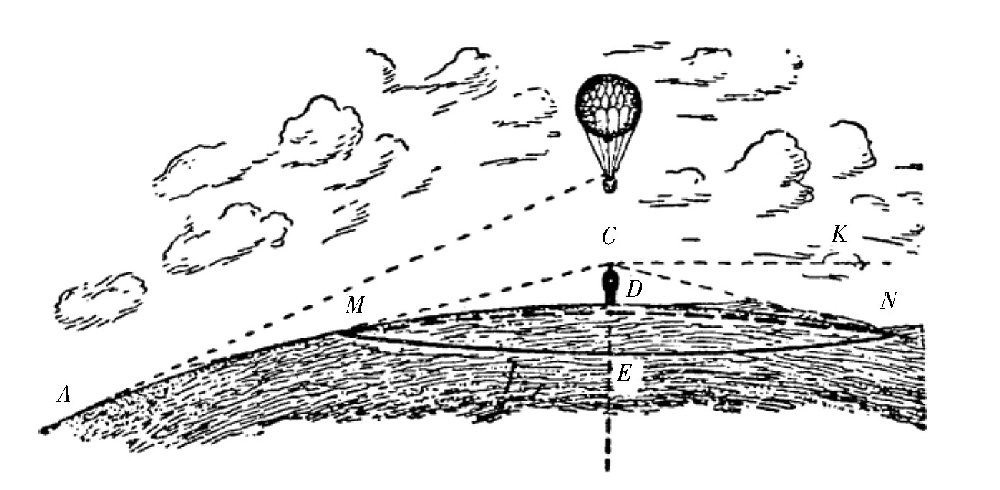
图 地平线。
你可能以为图中的情形跟实际有出入,因为当我们观察的时候,总是觉得地平线跟我们的眼睛是在同一水平面上的,而在图中,这个地平线的圆周明显比观察者的眼睛低。没错,在我们的感觉中,我们的眼睛跟地平线始终在同一水平面上,而且当我们的身体升高的时侯,还会感觉这个水平面也跟着一起升高了。实际上,这只是我们的错觉罢了。实际的情况是,地平线总是比我们的眼睛要低,就像图所画的那样。只不过,直线CM和CN跟垂直于地球半径的直线CK之间的夹角非常小,不可能用仪器测量出来罢了。
我们再来说一件非常有趣的事情。刚才我们说过,如果观察者的高度升高,比如,乘坐在飞机上,地平线好像还是跟他的眼睛在一个水平面上,地平线好像也跟着他升高了。如果飞机飞得非常高,观察者就会感到,好像飞机下面的地面都在地平线以下了,地面好像成了一个嵌到地面之下的盆,地平线就是这个盆的“边”。关于这种情形,在埃德加·爱伦·坡的幻想小说《汉斯·普法尔历险记》中,曾经有过详细的描写和解释。
小说的主人公航空家说:
最令我惊奇的是,在我看来,地球竟然凹下去了。刚开始我还以为,随着我逐渐升高,一定可以看到地球的凸面,没想到不是这样。我仔细想了一下,终于找到了这个现象的解释。如果从我乘坐的气球竖直向地球引垂线,这就相当于直角三角形的一条直角边,而这个直角三角形的底边就是从这条垂线和地面的交点到地平线的那条直线,斜边就是从地平线到气球的连线。但是,跟我看到的视野相比,气球的高度是非常小的,也就是说,刚才提到的这个三角形的底边和斜边比直角边要大得多,我们可以将三角形的底边和斜边看成两条平行线,所以在观察者看来,位于气球底下的每一个点,总是低于地平线。这就是我们总是觉得地球表面好像凹下去的原因。这样的情形会一直存在,除非地球达到了一个非常高的高度,那时候三角形的底边和斜边就不再是平行的了。
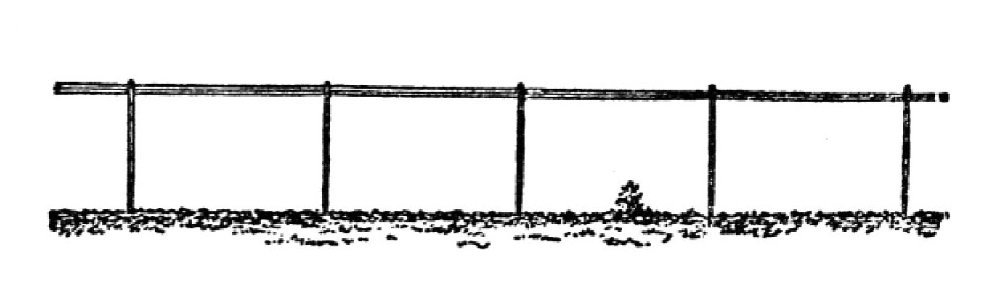
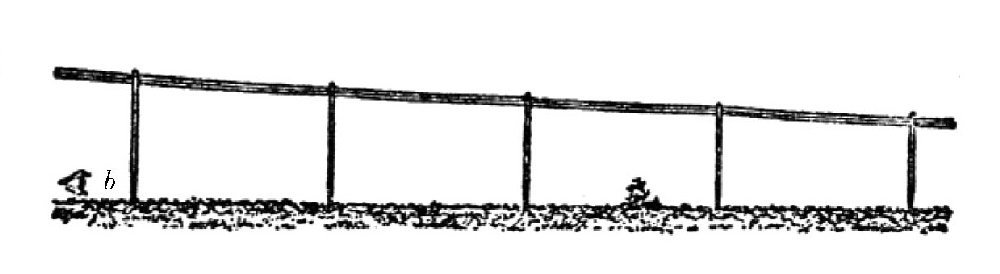
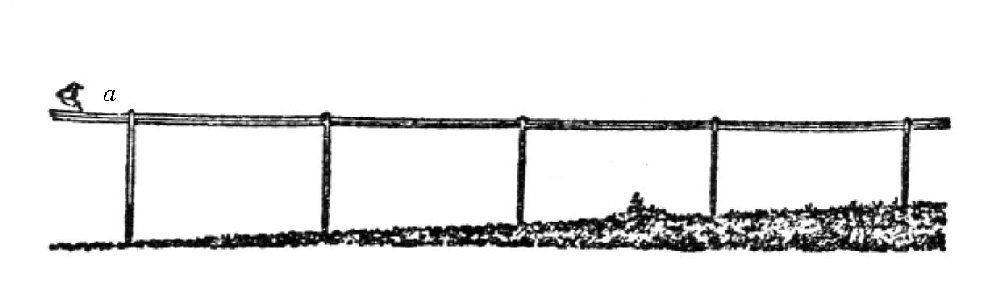
我们再来举一个例子,来帮助大家认识这一现象。如图所示,假设有一排整齐的电线杆。如果你的眼睛在电线杆的点b,也就是在电线杆脚的平面上,那么你看到的电线杆的情形就是图的样子。但是,如果你的眼睛放在点a,也就是在电线杆顶的平面上,那么你看到的电线杆的情形就是图的样子,这时候,地平线对你来说就好像升高了一样。