【题目】在牛顿的著作《普遍的算术》中,他这样写道:“在科学的学习中,题目比规则要有用多了。”因此,当他阐述一些理论的时候,总是会结合实例进行说明。在他所举的实例中,有一个关于牛在牧场上吃草的经典题目,下面介绍的题目就是从这个题目演化而来的:
“牧场上的草长得很均匀,每个地方都一样密,长得一样快。如果是70头牛在这片草地上吃草,24天就可以把草吃完;如果是30头牛,则需要吃60天。现在的问题是,如果想让草地上的
草吃96天,牧场上应该有多少头牛?(图)”

这是契诃夫的著作《家庭教师》中出现的题目,老师把这个题目布置给学生后,学生的两个成年亲戚帮着他做,但是花了很长的时间也没有得出结果,他们感到十分困惑。
其中一个亲戚分析道:“真是奇怪,如果70头牛花24天把牧场里的草吃完,那么要想在96天的时间里把草吃完,牛的数量就是70的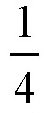
,也就是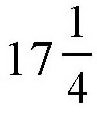
头牛。这肯定不对啊!再看后面:30头牛在60天的时间里把草全部吃完,那么,要在96天内把草吃完,就需要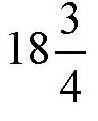
头牛,这也明显不对嘛。另外,如果70头牛在24天内把草吃完的话,30头牛要吃完这片草只需要56天,但题目却说需要60天。”
“你可能忘了考虑一个问题,草是一直在生长着的。”另外一个说道。
这个人说得很对,是的,草一直在生长,如果忽略这一点,不仅解答不出这个题目,而且你发现题目给出的条件也是自相矛盾的。
那么,该如何求解这个题目呢?
【解答】这里我们也需要用到一个辅助未知数,即每天长出的草与牧场上草的总量的比值。假设每天长出的草是y,在24天内长出的草就是24y。假设牧场上草的总量为1,那么24天内70头牛一共吃的草是
1+24y
70头牛每天吃掉的草是
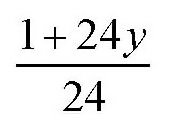
而一头牛在一天内吃掉的草就是
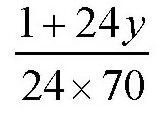
同样的道理,30头牛在60天内把牧场上的草吃完,那么一头牛在一天的时间里吃掉的草就是
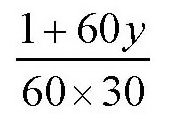
由于每头牛每天吃的草应该是一样的,所以
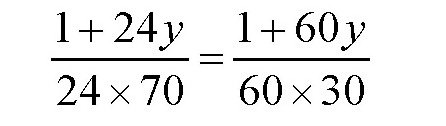
于是,可以得出
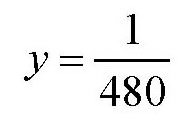
也就是说,每天长出的草是整片牧场上草总量的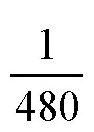
。根据它,我们可以计算出一头牛在一天当中吃掉的草占牧场上草的总量的比率是
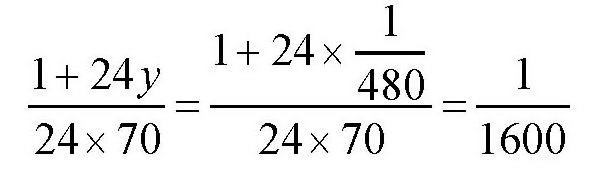
接下来假设题目所求的牛数为x,那么
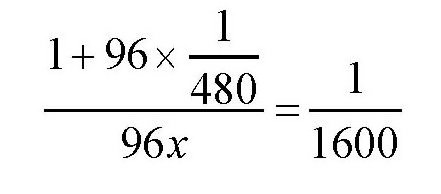
解得
x=200
因此,要想在96天的时间内把牧场上的草全部吃完,需要20头牛。
