推算生日,请你的朋友把他生日的日期乘以12,再把生日的月份乘以31,然后把两个数相加的结果告诉你,这时你就能推算出他的生日是几月几号,

【题目】下面来做一个游戏，看看你对不定方程的解答是否熟练。

请你的朋友把他生日的日期乘以12，再把生日的月份乘以31，然后把两个数相加的结果告诉你。这时你就能推算出他的生日是几月几号。

比如，如果你朋友的生日是2月9日，那么他会这么计算：

9×12=108，2×31=62，

108+62=170

所以，他告诉你的结果是170。通过这个数值，你要推算出他的生日，该怎么做呢？

【解答】根据题意，有下面的方程

12x+31y=170

其中x和y都是正整数，并且

x≤31，y≤12

于是

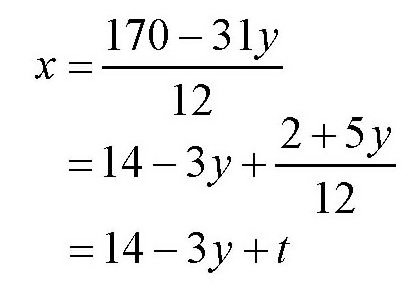
其中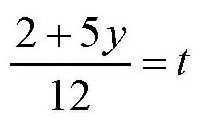

所以

2+5y=12t

从而

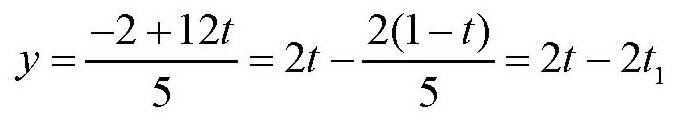
其中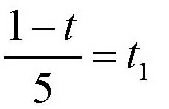

所以

1-t=5t₁

t=1-5t₁

从而

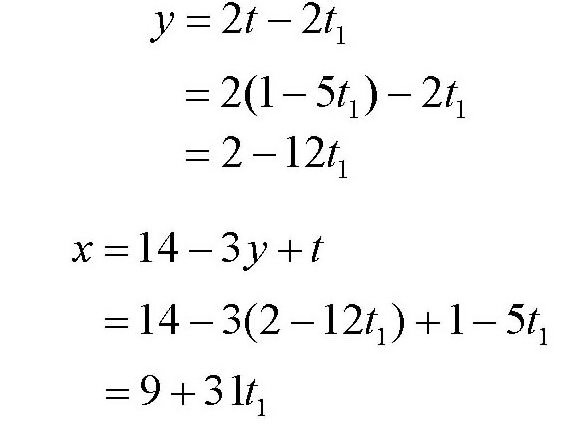
而

0<x≤31,00<y≤12

所以，t₁的取值范围是

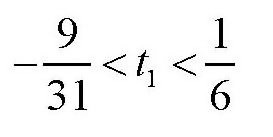
由于t₁是整数，所以t₁只能取0，于是

x=9,y=2

所以，你朋友的生日是2月9日。

事实上，这个游戏总能成功，因为这个题目的解只有一个。假设把你朋友告诉你的结果记为a，那么，我们有下面的方程

12x+31y=a

这里，我们采取“反证法”。假设上面的方程有两个解，分别是x₁，y₁和x₂，y₂，其中，x₁，y₁不大于31，y₁，y₂不大于12。那么，有下面的等式

12x₁+31y₁=a

12x₂+31y₂=a

两式相减，得到

12(x₁x₂)+31(y₁y₂)=0

由于x₁，x₂，y₁，y₂均为整数，所以我们可以得出12(x₁x₂)可以被31整除。而x₁,x₂都不大于31，所以，（x₁-x₂）也小于31。从而，只有在x₁=x₂时，₁₂12(xx)才能被31整除，也就是说，这两个解是相等的。这与前面的假设是矛盾的，换句话说，前面的方程有唯一的解。