介绍太多枯燥无味的公式,肯定会让一些物理爱好者觉得厌烦,但是如果不从数学的角度分析各种现象,我们就无法预见这些现象的发生条件及发生过程。比如,我们上一节所介绍的“魔环”现象,要想知道在怎样的条件下才能成功演出,就需要用数学公式来计算。对于这个题目,我们只需用到两三个公式。
按照图中的标示,我们现在就来进行一下计算。
在图中,我们分别用下面的字母来表示计算所需要的数值:
h:骑自行车的杂技演员出发地点的高度。
x :演员出发点比“魔环”最高点高出的距离(如图 4 1 所示, x = h -AB)。
r:环的半径。
m:演员与自行车的重量之和(单位为mg)。
g:地球的重力加速度(为9.8米/秒2)。
v:自行车到达环的最高点时的运行速度。
我们用两个方程式就能把这些数值联系到一起。首先,我们知道,自行车在下滑时,位于和B点一样高的C点处。自行车的速度与演员骑车到达顶点B时的速度相同。这个速度这样计算:

所以,到达B点时,演员的速度等于:

那么,演员要想达到环的顶点,而且不会摔下来,就要保证演员的向心加速度大于重力加速度:
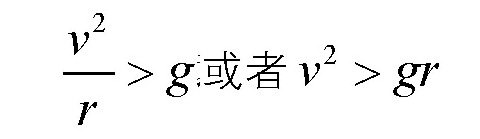
我们知道v2=2gx,可得:

通过计算,我们可以知道这个让人有点儿头晕的杂技表演要想成功,“魔环”的制造就要满足这样的条件:
“魔环”斜坡部分的最高点减去环的最高点所得的差要大于环半径的一半以上。
自行车行驶的坡度大小没有要求,只需要保证演员出发点比环的顶点高,高出的数值要达到环的直径以上就行。
由此可知,如果环的直径大小是16米,那么演员出发点的高度就必须高于20米才行。这些条件如果不满足,演员即使有再高超的技巧,也无法走完“魔环”,在还没到最高点的时候,就会掉下来。
这里要注意一个问题,我们并没有考虑自行车与环面之间摩擦力的影响。我们假定自行车行至B点和C点时的速度是相同的。要想无限接近这一点,自行车行驶的路就不能太长,斜坡也要陡一点儿。如果斜坡的坡度太小,自行车会因为摩擦力而减慢速度,那么它到达B点时的速度就比到达C点时的速度小了。
另外,需要指出的是,杂技演员在表演这个杂技的时候,自行车上是没有装链条的,他不需要也不能改变速度,演员是在重力的作用下向前行进的。所以如果自行车不是很正,只要稍微倾斜一点点,演员就可能从路上滑下去,然后被抛出去。演员骑着自行车沿着环行进的速度很快,他只需要3秒就能够走完长度为16米的环,也就是60千米/小时的速度。演员需要一定的技术才能这样高速驾驶自行车,但这种技术并不难掌握。在杂技表演手册中,对这种杂技有这样的描述:
只要设备足够坚固,计算绝对准确,自行车杂技本身并不危险。演员本身的表现决定了这个杂技是否危险。假如演员表演时紧张了,手抖动了,甚至失去了自我控制力,他就有可能会演砸,并发生事故。
有很多飞行特技也是利用这一条定律完成的。比如,飞机在表演翻跟头时,只要驾驶员能沿着曲线熟练地驾驶飞机,让飞机准确、快速地飞行,就可以成功。
