有时不可忽略的差别,旧力学和相对论力学的差别

在现实工作中，经常会碰到一些纯算术运算。有时候，我们不得不借助一些简单的代数方法，否则，运算起来非常麻烦。下面就来看一个例子：

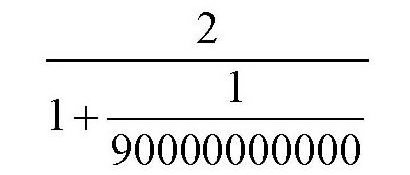
这个数值是多少呢？它有什么意义？在物理学中，这个数在相对论力学中有重要的意义。按照旧力学理论，如果一个物体同时参与同方向的两种运动，这两种运动的速度分别是v₁和v₂，那么总的速度就是（v₁＋v₂）。但如果在相对论力学中，这个总速度应该是下面的式子：

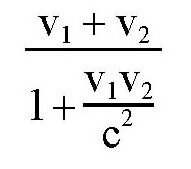
其中，c表示真空中光的传播速度，一般取300000千米/秒。如果v₁和v₂都是1千米/秒，那么按照旧力学理论，总速度是2千米/秒，而在相对论力学中，这个总速度是

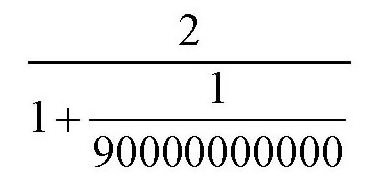
千米/秒。

这两个结果相差多少呢？从式子中可以看出，这个差别是很小的，能否用最精确的仪器测量出这个差别来呢？不妨先计算出这个差别到底有多大。

下面，用两种方法来计算上面的数值，一种是算术方法，一种是代数方法，看看哪种更简便。先来看算术方法。

把上面的分数变化一下，得到

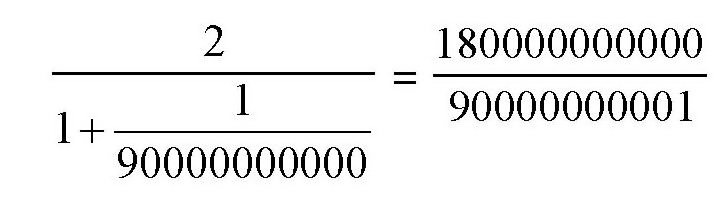
然后用分子除以分母：

可以看出，这种方法非常麻烦，不仅费时费力，还很容易弄错。而且，在计算的时候，必须看清楚最后得到的商中有几个9，到第几位的时候才变成别的数字。

下面来看一下如何用代数方法求解这个数值，该方法非常简便。

这里，先引入一个近似等式。如果一个分数a的值非常小，那么

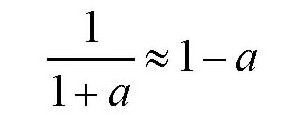
这个式子很容易证明，只要在式子的两边都乘以（1+a），就得到

1=(1+a)(1-a)

即

1=1a²

由于这里的a非常小，所以²a更小，可以忽略掉。

现在来计算一下上面的那个数值：

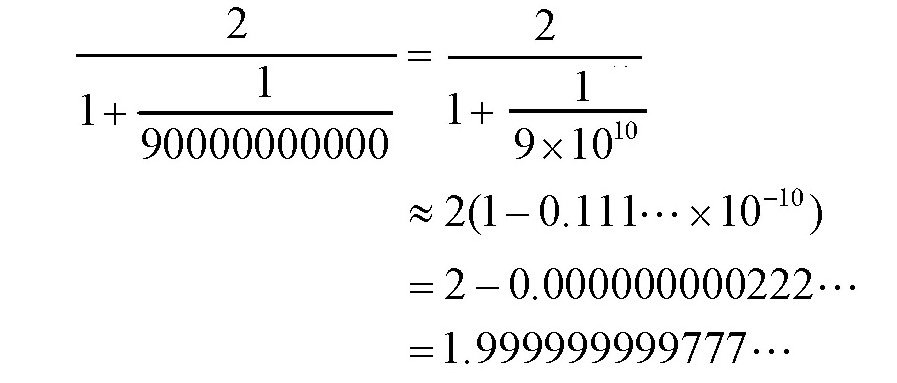
由此可见，计算出的结果是一样的，但后面的方法简便多了。如果读者对相对论力学感兴趣的话，就知道这个方法对于相关问题的研究具有重要意义。另外，这个结果告诉我们，常见的物体速度跟光的速度比起来，简直太小了，在旧的力学理论体系中，物体的速度可以叠加，我们根本感觉不到这一结果跟实际结果的差别。在上面的结果中，我们算到了小数点后第十二位数字，实际上即使用最精确的测量仪器也不过测量到小数点后第九位，一般精确到小数点后第三到第四位就足够了。所以，可以这么说，在爱因斯坦的相对论力学中，如果物体的运动速度比光速小得多，这一影响可以忽略不计。不过，在现实生活中，有一些领域需要进行精确的计算，比如说，在空间研究中，卫星或者火箭的运行速度已经达到10千米/秒，甚至更多，这时旧力学和相对论力学的差别就显示出来了。在现代科技中，这一差别已经体现在很多方面。