用4个2写一个最大的数是多少

【题目】把上面的题目扩展一下，来看看4个2的情形。

不使用运算符号，把4个2摆成尽可能大的数，该如何摆放呢？

【解答】4个2所有可能的摆法一共有8种，即

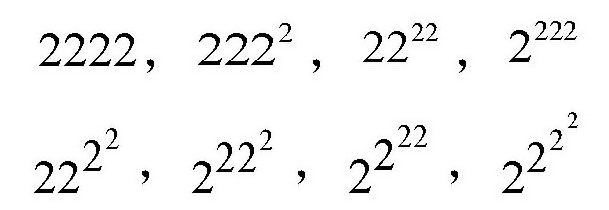
在这几个数中，到底哪个数最大呢？

首先来看最上面的4个数，也就用两层摆法得到的数。

很明显，第一个数字2222，比后面的3个数都要小。先比较一下2222后面的两个数：222²和22²²。

把22²² 进行如下变换：

22²²=22^2×11=(22²)¹¹ =484¹¹

与222²比，484¹¹的底数和指数都要大得多，所以，22²＞222²。

再来比较22²² 和第一行的第4个数2²²²。我们取一个比22²²更大的数32²²，下面就来证明，即使是32²²，也比2²²²小。

实际上，

32²²=(2⁵) ²²=2¹¹⁰

这个数比2²²²小多了。

也就是说，在第一行的4个数中，2222 最大。

再来看第二行中的几个数：

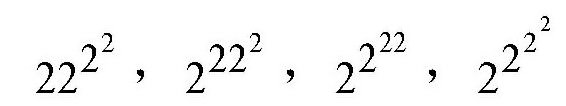
显然，最后一个数等于216，它肯定不是最大的，直接淘汰掉。而第一个数22²² ＝22⁴ ，它小于32⁴＝2²⁰， ，也就是说，这个数也比中间的两个要小。所以，最后就变成比较这3个数的大小：

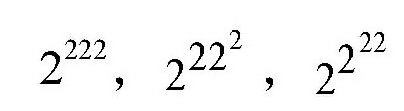
这三个数都是以2为底的指数，所以，只需要比较下面3个指数

222，484和2²²

的大小即可，指数最大的对应的数就最大。

很显然，2²²比222和484都要大得多。

因此，用4个2摆成的最大的数是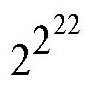

。来估算一下这个数有多大。

由于

2¹⁰≈1000=10³

而

2²²＝（2¹⁰）²×2²≈4×10⁶

所以

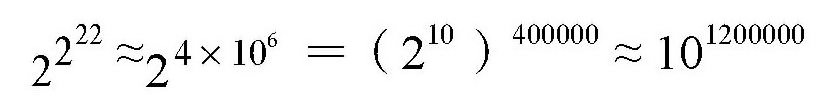
也就是说，这个数的位数比100万还要多。

1战术的形式多种多样，此处只是其中一种。战术不同，计算机的下棋方法自然也就不同。

2水平很高的棋手，通常会考虑未来10步甚至更多步的情况。