在很多“永动机”的设计中,有相当一部分是以物体在水里的浮力原理来设计制造的。现在,我们来谈谈其中的一种。
有一个装满水的高塔,高为20米,高塔的上下两头各有一个滑轮。制造者把一条坚固的循环带样的钢绳绕在了滑轮上,而钢绳上还有14个边长为1米的空的方箱子,这些箱子都是用铁皮做的,密闭性很好,不会透水。图和图所示就是这种高塔的外观图和剖面图。

图 “水塔永动机”的外观图。
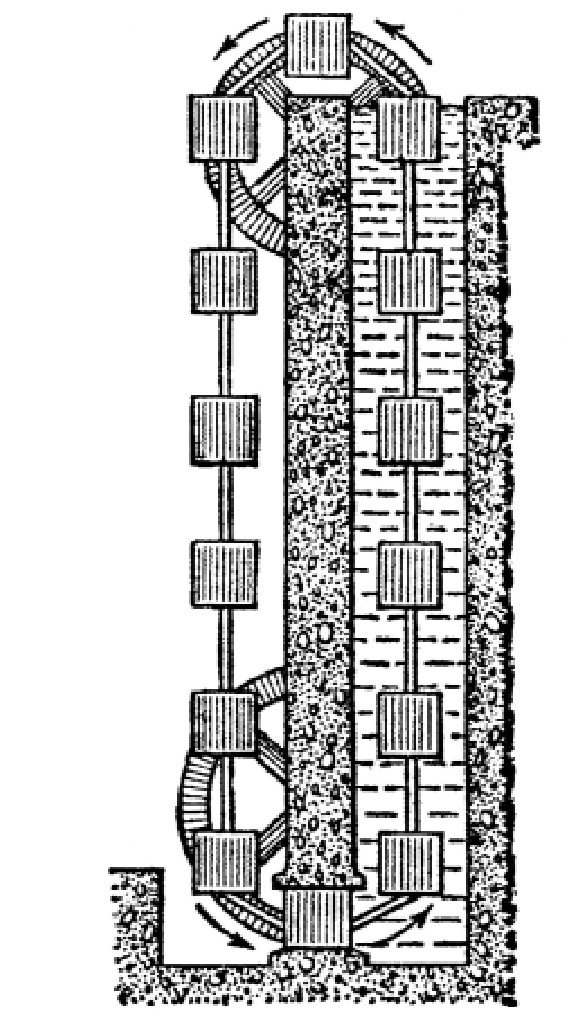
图 “水塔永动机”的构造图。
这种装置是怎样工作的呢?熟悉阿基米德原理的人可能都会这样想:一开始,水里的箱子在排开的水的重量之后,会浮向水面。浮力的大小就是被排开的1立方米水的重量乘以浸在水里的铁箱的数量。从示意图中可以看到,总共有6个箱子是浸在水里的。就是说,有相当于6立方米水的重量大小的浮力(也就是6吨)在拉动铁箱上浮。当然,铁箱本身也有重量,这部分重量试图把它们拉向水底,但是还有6个自由下垂的铁箱挂在高塔外面的绳索上,所以两边的力量是平衡的。
如此一来,绳索就会始终承受着6吨向上的拉力,然后按照上述方法不停地转动。很显然,绳索会在这个拉力下,一直在滑轮上滑动,不会停下来。而它每转一圈所做的功的大小是:6000×10×20=1200000焦耳(g=10)。
这样的话,假如一个国家遍布这样的塔,那么这些塔会给国民提供无穷的功,以满足整个国民经济的需要。发电机用动力塔来转动,就能得到无穷无尽的电能。
但事实并非如此,这个设计根本经不起推敲。仔细研究,你就会发现,绳索根本就动不起来,下面我们就来仔细分析一下其中的原理。
要想让这根静止的绳索转动起来,这些铁箱就必须能够从下面进入水塔,再从水塔上面离开。但是铁箱想要从下面进入水塔,就不得不克服来自20米高的水塔的压力。这个压力作用在每1平方米的铁箱上的大小恰好是20立方米水的重量,也就是20吨。上文说到,铁箱受到的向上的牵引力只有6吨,这个牵引力显然不能把铁箱拉到水塔里面去。
“发明家们”设计了无数的“水力永动机”,虽然他们的设计没有取得成功,但其中不乏巧妙的构思。
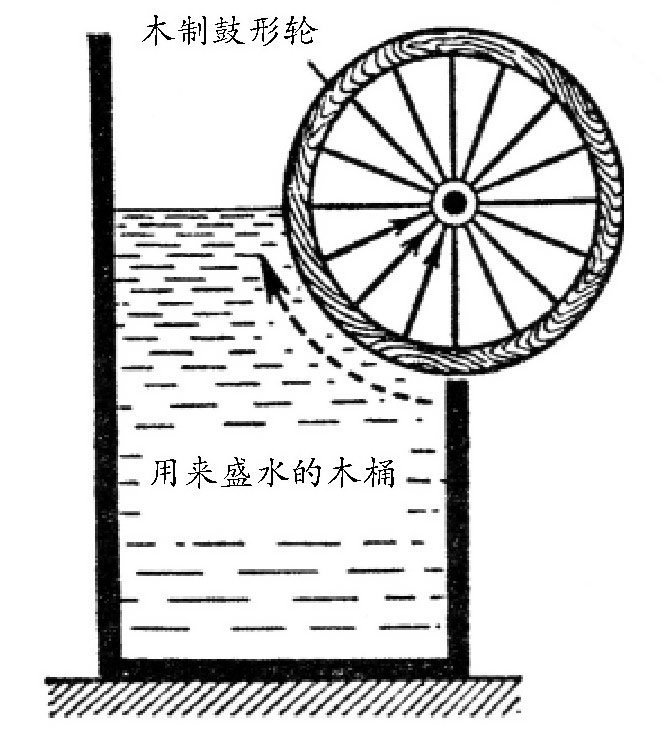
图 另一种“水力永动机”。
我们来看 图 。这是另一种水力永动机的设计图。一只木制鼓形轮装在轴上。轮的一部分一直浸在水里。如果阿基米德原理是正确的,那么浸在水里的那部分就必然会上浮,而且只要水的推力能够克服轮轴上的摩擦力,那么鼓形轮就会不停地转动。
这个设计是不是看着很有道理?可不要着急制造这个水力“永动机”!因为鼓形轮根本不会转动,你一定会失败的。我们的推理哪里不对?是我们没有把各种作用力的方向考虑周全。这些作用力永远是垂直于鼓形轮表面的,和所有通往轴的半径方向相同。按照我们的生活经验,顺着轮子的半径去施加压力,轮子是不可能转动起来的。要想使轮子转动起来,就需要沿着轮子的圆周切线方向施加压力。现在,读者们应该就很容易理解:“永恒运动”为什么总是以失败告终了。
那些想发明“永动机”的人,从阿基米德原理那里得到了诱人的“精神食粮”。他们总是不遗余力地将那些好像失去的重量当作机械能的永恒动力,所以他们确实也设计出了很多非常巧妙的装置。
