前面那个题目是从牛顿原来的题目改编而来的,下面我们就来看一下牛顿著作中的那个题目。
有3个牧场,它们的面积分别是
公顷,10公顷,24公顷。这几个牧场上的草长得都一样密、一样快。在第一个牧场饲养12头牛,里面的草可以吃4个星期;在第二个牧场饲养21头牛,里面的草可以吃9个星期。那么,在第三个牧场饲养多少头牛,里面的草才能恰好够吃18个星期?
【解答】跟前面一样,此处我们引入一个辅助未知数y,用来表示在1星期内每公顷牧场上新长出的草占原来草的总量的比重。首先来看第一个牧场,在1星期内新长出的草是1公顷牧场上原有草总量的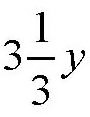
倍,在4个星期里,新长出的草就是1公顷牧场上原有草总量的
倍。
这就相当于第一个牧场的面积变大为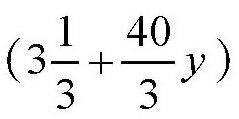
公顷。
也就是说,牛在4个星期内吃掉了牧场上面积为
公顷的草。那么,这12头牛在1个星期内吃掉的草为上数的
,进而,1头牛在1星期的时间内吃掉的草就是上数的
,即

也就是说,1头牛在1星期的时间内一共吃了
公顷这么大面积的牧场上的草。
同理,可以计算出在第二个牧场上1头牛在1星期的时间内,能吃掉多大面积的牧场上的草。
在1个星期里,1公顷牧场上长出的草是y;
在9个星期里,1公顷牧场上长出的草是9y;
在9个星期里,10公顷牧场上长出的草是90y。
因此,21头牛在9个星期内吃掉的草,相当于面积为(10+90y)公顷的牧场上的草。
从而,1头牛在1个星期内吃的草为
公顷。
由于每头牛每个星期的吃草量是相同的,所以

很容易求出

有了这个数值,下面就可以计算出1头牛在1个星期内的吃草量,即

接下来就很容易求出题目所求的量,假设第三个牧场上牛的数量是x,那么

解得x=36。也就是说,在第三个牧场上饲养36头牛的话,里面的草就可以恰好够吃18个星期。
