【题目】如图所示,在一堵竖直的墙壁上画一个圆圈,这个圆圈的直径是1米。从圆圈顶点A沿弦A B 和 A C 分别装有两道滑槽。从点A处同时放下三颗弹丸,其中一颗竖直自由下落,另外两颗沿两道滑槽下落。假设滑槽里面没有摩擦力,那么哪颗弹丸会先落到圆周上呢?
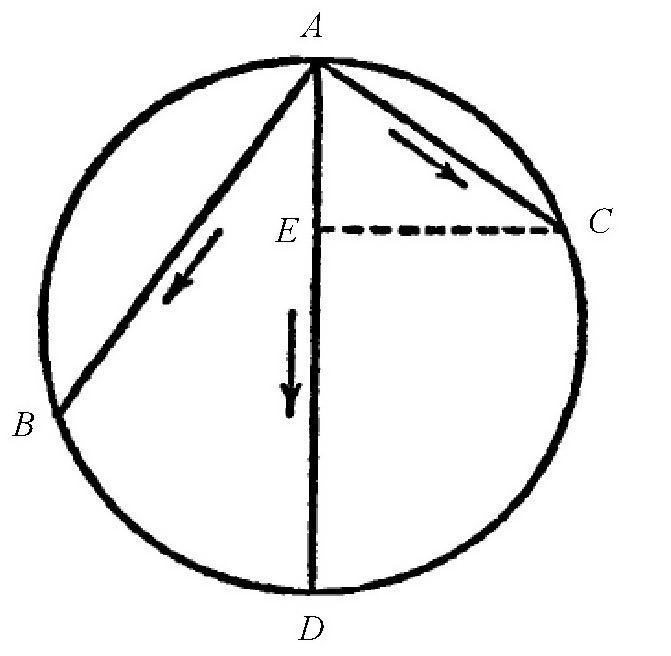
图 三颗弹丸的滑落轨道。
【解答】图中的3条路径,滑槽AC是最短的,所以人们通常以为:从滑槽AC下落的弹丸最先到达,而从滑槽AB下落的弹丸第二个到达,竖直AD下落的弹丸最后到达。
但是,通过实验证实,这三颗弹丸是同时到达的。
这是为什么呢?其实,原因很简单。虽然三颗弹丸走过的距离不同,但是它们的运动速度也不同。运动得最快的是竖直下落的那颗弹丸,而在滑槽坡度比较缓的AC上行进的弹丸,它的下落速度最小。也就是说,弹丸下落的距离越远,运动的速度越快。下面,我们就来证明一下。
对于竖直下落的弹丸来说,它下落的时间t可以用下面的公式计算:
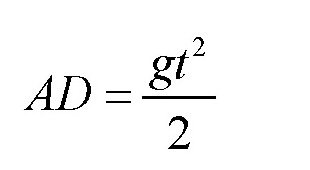
可得:
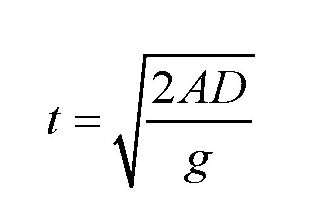
而沿滑槽AC下落的弹丸的运动时间t1为:

其中,a为沿滑槽AC运动的弹丸的加速度。我们很容易可以看出:

可得:

由图,我们可以知道:
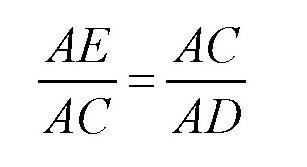
可得:

可得:

也就是说,从滑槽AC下落的时间t1等于竖直下落的时间t。同样的,我们还可以得出:从滑槽AB下落的时间也等于竖直下落的时间t。
其实,对于这个题目,我们还可以换一种方式求解。如 图 所示,三个弹丸分别从圆周上的三个点A、B、C同时沿着滑槽下滑,哪个弹丸最先到达点D处?

图 伽利略的题目。
对于这个变形题目,相信读者可以很轻松地计算出来:这三个弹丸是同时到达点D处的。
伽利略在其著作《关于两个新的科学学科的谈话》一,提出了这个题目,并进行了详细的解答。同时,在这本,伽利略还最先提出了物体下落定律。
此外,在这本,我们还可以找到这个定律:“如果从高出地平线的一个圆的最高点,分别引出到圆周的不同的倾斜平面,那么物体在这些面上的下落时间是相同的。”
