喜欢动手制造东西的人 ,比如,无线电爱好者、模型设计者,或者别的创造者,在实际工作中,经常会碰到下面这些需要动脑筋的题目。
【题目】从一块铁片上割出一个正多边形,边数是任意指定的。
其实,这个题目跟下面的题目是一样的:把一个圆周平均分成n份,这里的n是整数。
【解答】我们暂且把量角器放到一边,不使用它。因为这毕竟是一种“用视觉”来解决问题的方法。下面我们试着用几何的方法解决,也就是只用直尺和圆规。
首先,我们先考虑这么一个问题:从理论上说,只用直尺和圆规,可以把一个圆周平均分成多少个相等的部分呢?其实,关于这个问题,数学上已经给出了正确的答案,也就是说,并不是所有的数字都可以。这些可以实现的数字是:
2、3、4、5、6、8、10、12、15、16、17……257……
而下面的数字是不可以实现的:7、9、11、13、14……
还有更糟糕的,对于这类题目,并没有一个固定的作图方法。比如,分成15等分和12等分的方法是不同的。而且,这些方法并不是那么容易记住。
所以,在实际工作中,非常需要找到一种几何学方法,哪怕只是求出近似值,只要方法比较简单就行。
不过,很可惜,在几何学课本中,并没有注意到这一问题。下面,我们就来介绍一个解答这类题目的有意思的近似方法。
如 图 所示,把图中给出的圆周平均分成9部分。
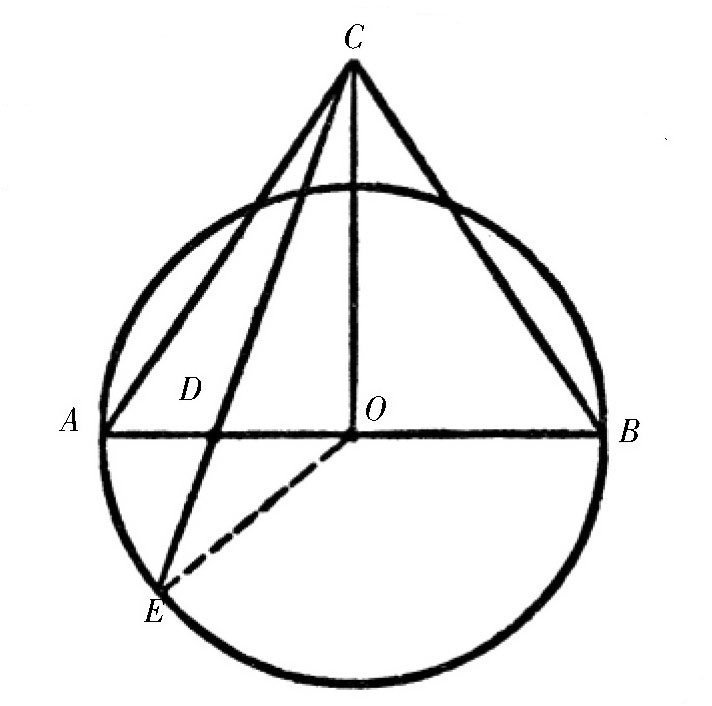
图 把圆周n等分的几何学近似法。
任取一直径AB,用圆规作一等边三角形ACB,在直径AB上取一点D,使AD∶AB=2∶9。(一般遇到这类问题的时候,我们都把这一线段分成2∶n)。
连接点C和点D,并延长至圆周上的点E,那么弧线AE就大概等于圆周长度的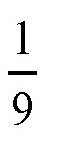
,或者说,弦AE就是内接正九边形的一条边。它的误差大概是0.8%。
把刚才作图中的圆心角AOE和等分数n的关系用算式表示出来:
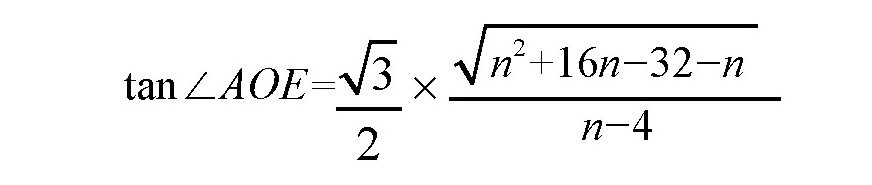
如果n的数值比较大,上式可以简化为:

从另一种意义上说,要想把圆周准确地划分成n等分,那么圆心角AOE应该是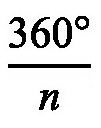
。把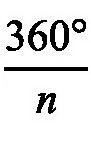
和角AOE进行比较,就可以得到误差的大小。
在下表中,我们列出了一些n值对应的误差。
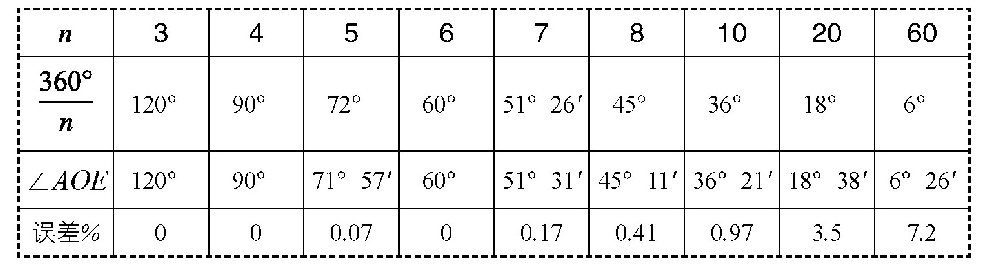
由上表我们可以知道,如果采用上面的方法把一个圆周平分成5、7、8、10部分,误差并不是很大,只有0.07%到1%。对于这么小的误差,在实际情形下,并不会有什么影响。但是,如果这个n值比较大,这个方法的精确性就不是很好了,误差就会比较大,不过,最大也不会超过10%。
