我们都知道,由于受到地球的引力,所有位于地球上空的物体都会被吸引到地球上来。但是,为什么人造卫星可以在太空飞行,却掉不下来呢?这是因为,运载人造卫星的火箭是多级的,它给了人造卫星一个非常大的速度,大概是8千米/秒。
如果一个物体以这么大的速度飞行,它就不会被吸引到地面上,而是会变成人造卫星。在地球引力的作用下,它将围绕地球做曲线运动。确切地说,它是沿着一个封闭的椭圆形轨道运动的。
其实,在某些情况下,卫星的轨道也可以是一个围绕地球的圆周。下面,我们不妨来计算一下,卫星的运行速度到底是多少。
人造卫星在圆周轨道上飞行时,受到了向心力的作用。当然,这里的向心力其实就是地球的引力。假设人造卫星的质量为m,它做圆周运动时的速度为v,轨道半径为R,那么向心力F可以表示为下面的式子:

根据万有引力,可知:
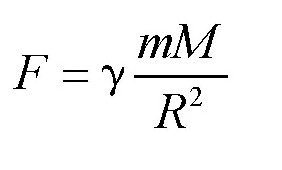
其中,M 表示地球的质量, 表示引力常数。
由这两个式子可得:
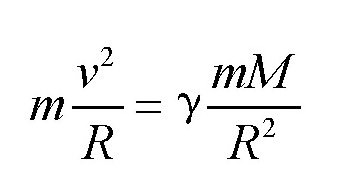
速度v的值为:
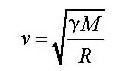
如 图 所示,假设卫星距离地面的高度为H,地球的半径为r,那么上面的式子就可以变化为:

图 人造地球卫星在距离地面的H高度上做圆周运动。
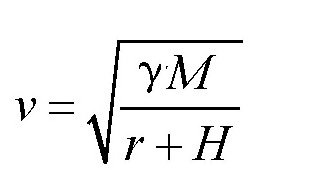
为计算简便, 我们还可以对上面的式子再进行一下变化。我们知道,地面上的物体受到的引力都为mg,也就是:

可得:
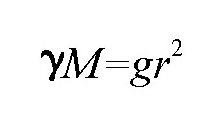
进一步可以得出:
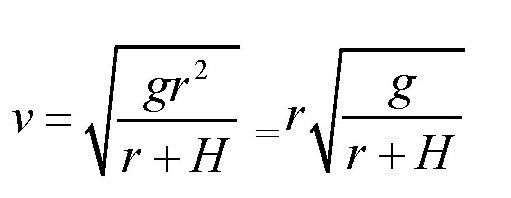
上面公式中的g是地面的重力加速度。
如果公式中的H比较小,跟地球的半径比起来可以忽略不计,我们可以认为H=0,上面的公式就可以简化为:
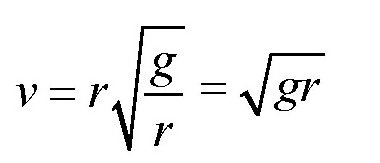
一般情况下,我们取重力加速度g=9.81米/秒2,地球半径r=6378千米。把这两个数值代入公式,就可以得到第一宇宙速度:

也就是说,当人造卫星围绕地球做圆周运动时,它的速度是7.9千米/秒。当然,由于地球的表面凹凸不平,又存在空气的阻力,人造卫星是不可能完全沿着圆周轨道运动的。如果增高圆周轨道的高度,那么人造卫星的速度就会小一些。
