一位物理学家说过:“有一天,我坐火车旅行,当火车转弯的时候,我突然发现铁路旁边的树木、房屋、工厂烟囱等都变得倾斜了。”
如果读者朋友乘火车的时候也注意一下,肯定也会见到这样的景象。
对于这个现象,该如何解释呢?难道是在转弯的这个地方,一条铁轨比另一条铁轨高一些吗,所以火车才倾斜着前进吗?当然不是。如果这时你不是在车内往外看,而是把头伸出窗外看周围的景物,你也会有同样的错觉。

在前面一节中,已经进行了一些类似的分析,所以我们在这里不再解释具体的原因。我相信,读者朋友一定也注意过这样的现象:当火车转弯的时候,悬挂在车顶上的悬锤或者其他物体,一样会变成倾斜的状态。也就是说,这时有了一条新的竖直线,它代替了原来的真正的竖直线,而本来处于竖直状态的物体则变成倾斜的了。
如图所示,我们可以计算出竖直线的新方向。图中,P为重力,R为向心力。它们的合力为Q(也就是乘客感觉到的重力)。车上的任何物体都会向这个方向倾斜过去。这个新的方向与原来的竖直线之间的夹角可以根据下面的式子来计算:
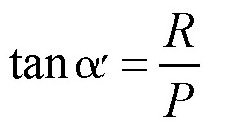
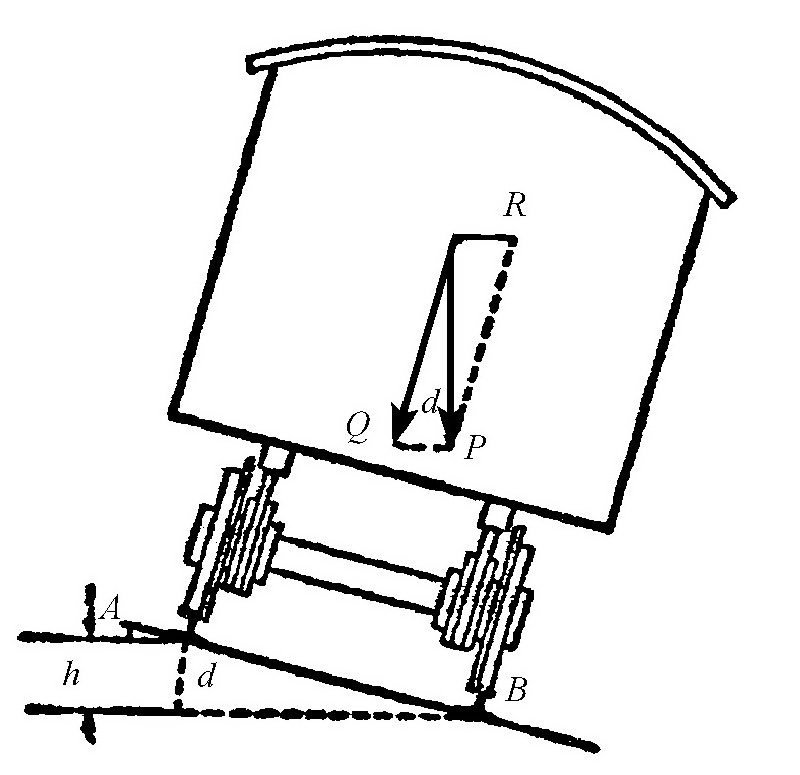
图 上部分为火车在转弯的时候,受到的力的示意图。下部分为铁轨截面的斜倾高度示意图。
而力R与向心加速度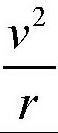
成正比。其中,v表示速度,r表示转弯处的曲率半径。由于力P与重力加速度g成正比,可得:
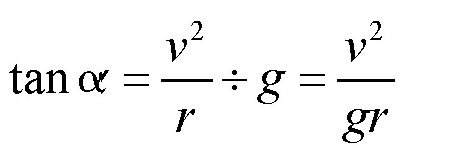
假设火车的速度为18米/秒,转弯处的曲率半径为600米,可得:
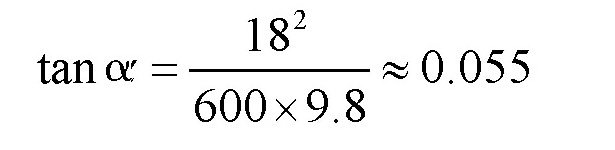
可得:
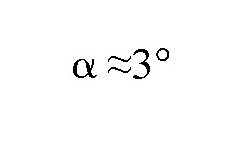
也就是说,我们以为的这个新的竖直线跟真正的竖直线之间的夹角为3°。在一些转弯半径比较小,或者转弯比较多的情况下,如果在火车上望向窗外的景物,看到的竖直景物可能会偏离10°,甚至更多。
要想让火车在转弯的时候仍然保持平稳,在铺设铁轨的时候,就需要在转弯的地方把外面的那条铁轨铺得高一些,至于需要高出多少,需要根据倾斜的角度来确定。比如,在刚才图的例子中,转弯处的外面一条铁轨应该比里面的那条高多少呢?假设高度差为h,我们可以根据下面的式子来计算:
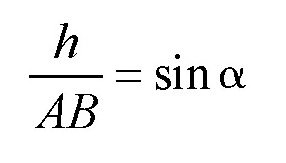
其中,AB表示两条铁轨之间的距离,一般为1.5米,而这里的角α的角度已经知道是3°。
sinα=sin3°=0.052
可得:
h=ABsinα=1500×0.052≈80(毫米)
也就是说,外面的铁轨应该比里面的高出80毫米。当然了,这个高度差只适用于一定的行车速度,并不适用于所有的行车速度,所以在真正铺铁轨的时候,通常根据一般的行车速度来进行设计。
