【题目】有三姐妹带着母鸡到集市上去卖。第一个人带了10只,第二个人带了16只,第三个人带了26只。上午,她们卖出的价格是一样的,都卖出了一部分母鸡。到了下午,她们卖出的价格仍然一样,只不过比上午低一些,最后把所有的母鸡都卖完了。她们卖得的钱数一样,都卖了35卢布。
请问,她们在上午和下午卖出的价格分别是多少?
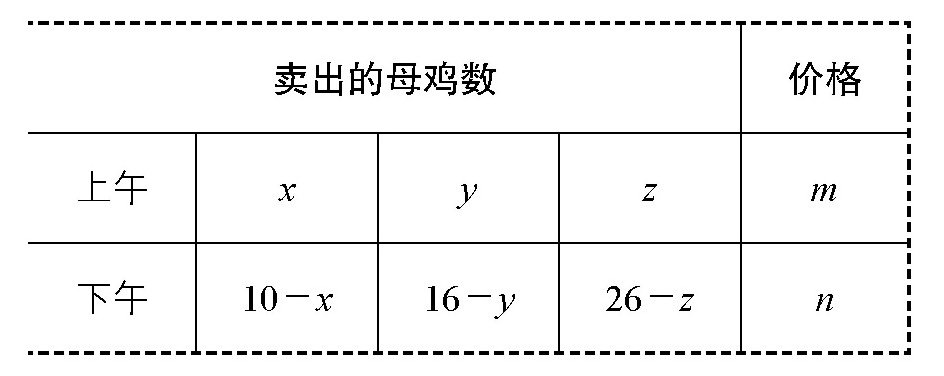
【解答】假设她们上午卖出的母鸡数分别是x,y,z,那么,下午卖出的母鸡就分别是(10-x),(16-y),(26-z)。再假设上午每只母鸡卖出的价格是m,下午每只母鸡卖出的价格是n,那么,可以得到下面的表格:
第一个人卖得的钱数为
mx+n(10-x)
第二个人卖得的钱数为
my+n(16-y)
第三个人卖得的钱数为
mz+n(26-z)
根据题意,她们卖得的钱数都是35卢布,所以,可得下面的
方程组
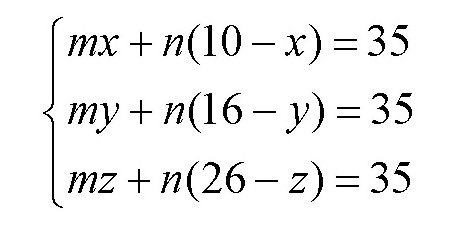
将每个方程变化一下,得到
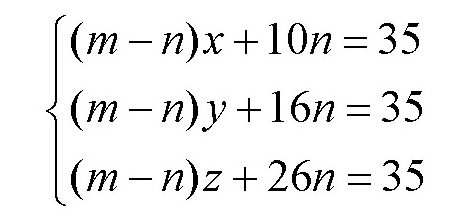
用第三个方程分别减去第一个方程和第二个方程,得到
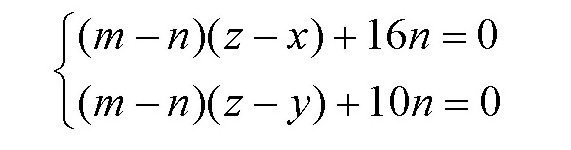
化简后可得
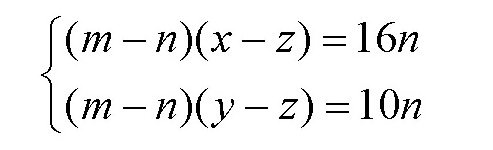
两个方程相除,得到
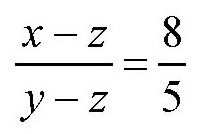
即
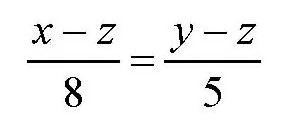
由于x,y,z都是正整数,所以它们的差也是整数。要想上面的等式成立,需要满足下面的条件:(x-z)能被8整除,(y-z)能被5整除。假设
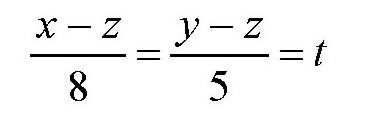
则
x=z+8t
y=z+5t
由于x>z(否则,第一个人不可能与第三个人卖的钱数一样多),所以t一定是正整数。
而x<10,所以
z+8t<10
其中z和t都是正整数,满足这一条件的z和t值是唯一的,它们都取1。
把z=1,t=1代入前面的方程
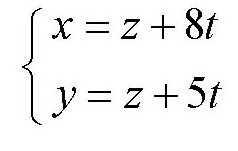
容易得出
x=9
y=6
再把x,y,z的值代入前面的方程组
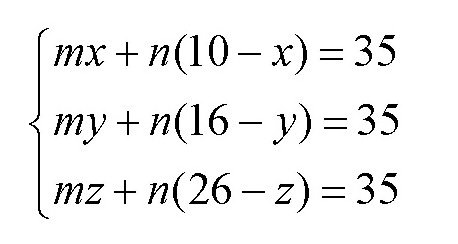
容易得出
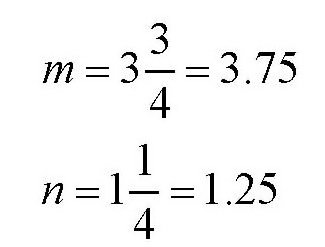
即她们上午卖出的价格是3.75卢布,下午卖出的价格是1.25卢布。
