在科幻小说《从地球到月球》中,要把一个活人用炮弹送到月球上。在当时,作者的这一想法太大胆了。不仅如此,作者儒勒·凡尔纳 还对这一想法进行了生动逼真的描述,好像是真的一样。很多读者读了这篇小说后,甚至会想,这个想法真的只是一个幻想吗?这真是一个有趣的问题。
从理论上来说,我们射出一颗炮弹,能否让炮弹一直向前飞,而不是在飞行一段时间后落回到地球上?答案是确定的。炮弹要是水平射出,就会落到地球上,这是因为炮弹被地球“吸引”了,正是有了引力的存在,使得炮弹不能一直直线飞行,飞行路线向下弯曲了。炮弹飞行的路线比地球表面弯曲的程度大得多,所以炮弹终究要落到地球上。那么,如果炮弹的飞行路线和地球表面的弯曲程度一样,这颗炮弹就会一直向前飞去,也就是沿着地球的同心圆飞行。从某种程度上说,跟月球一样,变成了地球的一颗卫星。
说到这儿,又遇到另一个问题:怎么才能使炮弹的飞行曲线跟地球表面的弯曲程度一样呢?答案其实很简单,只要炮弹飞行的速度足够大就可以了。如图所示,我们把炮弹放在山峰上的点A。如果不考虑地球引力,将炮弹水平向方向射出,飞行1秒钟后,应该到达点B。正是由于有了地球引力,在引力的作用下,炮弹飞行1秒钟后,到达的不是点B,而是点C,点C在点B下方5米。前面我们曾分析过,自由下落的物体,在第1秒里下落的距离正好是5米。我们不妨假设,点A到地球的距离和点C到地球的距离相等,也就是说,炮弹在这1秒的时间里,沿着地球的同心圆飞行。从图中可以看出,只要我们求出线段AB的长度,就可以得出炮弹在1秒钟的时间里飞行的距离。这样我们就得到了炮弹应该用多大的飞行速度飞行,才能保证不落到地球上来。
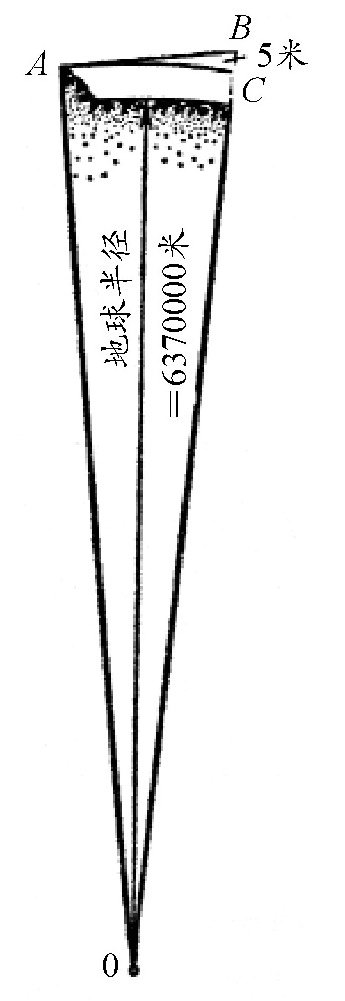
图 让炮弹脱离地心引力的速度计算图。
通过三角形AOB,利用勾股定理,OA是地球半径,约为6370000米,OA=OC,BC=5米,因此,OB=6370005米。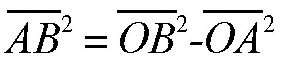
我们可以很容易计算出,线段AB的长度是8千米。
如果我们不考虑空气的阻力,只要炮弹的飞行速度达到8千米/秒,它在飞行的时候就永远不会落下来,而是围绕着地球旋转飞行。
设想一下,如果炮弹的飞行速度超过8千米/秒,会发生什么?有人计算过,如果速度超过8千米/秒,达到9千米/秒,甚至10千米/秒,炮弹的飞行轨迹就是一个椭圆,炮弹射出的初速度越大,椭圆的长轴越长。如图 所示,如果飞行速度达到11千米/秒以上,炮弹的飞行轨迹将不再是封闭的曲线,而是“抛物线”或者“双曲线”,也就是说,炮弹再也飞不回来了。
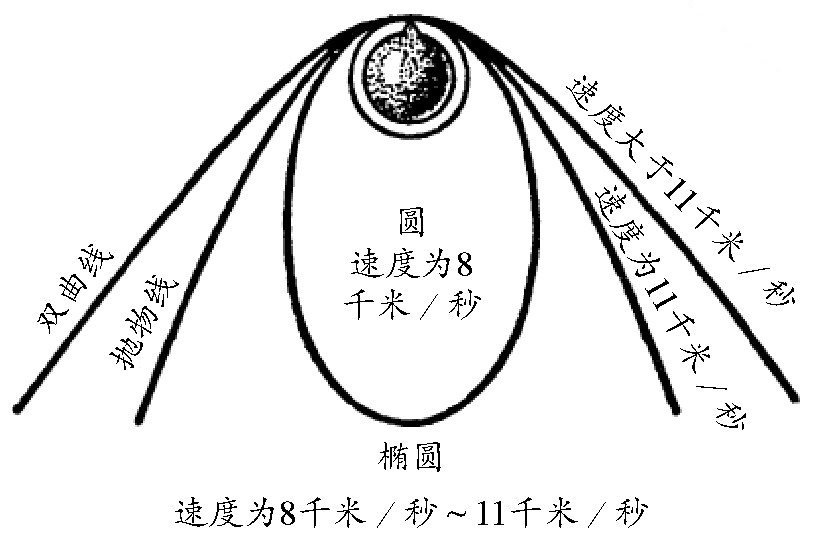
图 如果飞行速度达到11千米/秒,炮弹的飞行轨迹将不再封闭。
通过前面的分析,我们看到:理论上,只要炮弹的速度够大,乘坐炮弹去月球旅行,并非难事。
这里,我们假设空气阻力不存在。因为如果有空气阻力,很难达到这么高的速度。
