托尔斯泰曾经写过一本叫《读本第一册》的书,其中有这样一段内容:
一辆火车正在铁路上飞速前进。在一个铁路和马路交叉的地方,有一辆马车停在那里,车上载着重物,马车的旁边站着一个汉子,他想赶着马车通过铁路,但是由于马车的一个轮子掉了,所以马根本拖不动车子。火车上的乘务员看到这个情况后,便向火车司机喊道:“快煞车。”可惜,火车司机根本不听他的。他是这么想的:这时候,火车根本停不下来,而那个汉子又不可能把马车赶走。这样的话,火车根本就没办法避开马车。于是,他没有停下火车,而是让火车以最快的速度冲了过去。那个赶马车的汉子吓得赶紧让开了,火车就这样开了过去,并且车身没有受到任何震动。而马车却像木片一样,被抛到了一旁。火车司机对乘务员说:“现在,我们只损失了一匹马和一辆马车,如果按照你说的做,整辆火车上的人都会受到伤害,乘客甚至会全部遇难。这是因为,如果火车行驶的速度非常快,就可以把马车撞开,并保证火车不受震动;而如果以低速前进,火车就可能会脱轨。”
根据力学原理,这件事是否解释得通呢?显然,这里的火车和马车是两个不是“完全有弹性”的物体。在相撞的时候,被撞的马车在碰撞之前是静止的。假设火车的质量和速度分别是m1和v1,马车的质量和速度分别是m2和v2(v20),那么根据前面的公式,可得:
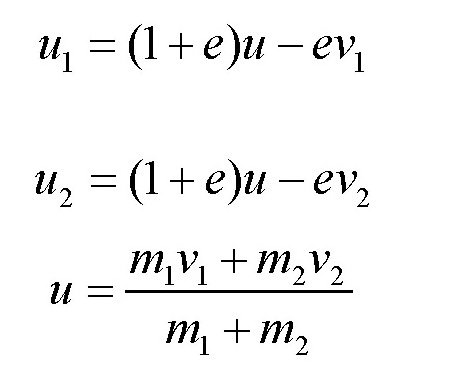
可得:
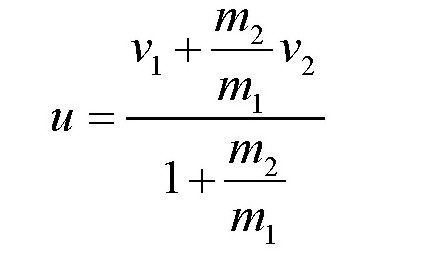
由于马车的质量很小,所以马车的质量m2跟火车的质量m1之比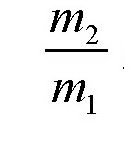
非常小,可以忽略不计,于是,我们可得:
u≈v1
代入上面的第一个式子,可得:
u1=(1+e)u-ev1=v1
也就是说,在相撞以后,火车仍然以原来的速度前进,所以对于乘客来说,根本感觉不到任何震动。
而马车呢?相撞以后它的速度将变成:
u2=(1+e)u-ev2=(1+e)v1
可见,马车的速度比火车还要大得多。火车在相撞以前的速度越大,马车在相撞以后得到的速度就越大,即马车被撞的力量也就越大。关于这一点,有非常重要的意义:为了避免火车事故,必须克服马车的摩擦力,要是碰撞的力量不够大,马车就会停在钢轨上,造成重大的火车事故。
从刚才的分析可以看出,火车司机的处置是正确的。正是因为他把火车以最快的速度开了过去,才使得马车和马被撞离钢轨,火车上的乘客也没有感觉任何震动。需要指出的一点是,在托尔斯泰那个时代,火车的速度并不是很大。
