如果你正好站在一条公路的转弯处,你能测出它的半径吗?
相比纸上的弧线半径来说,这个要复杂一些。如果是在纸上,解答起来会很简单:只需要从两条任意的弦的中点分别作一条垂线,垂线的交点就是这一段圆弧的圆心。从圆心到曲线上任意一点的距离就是所求的半径。
而对于公路来说,并不是可以很方便地作出图来的,因为公路曲线的中心可能在转弯处1000米~2000米之外,经常没有办法实地测量。当然,我们也可以把它画到纸上来求解,只不过要把它画出来并不简单。
下面,我们介绍一种方法,根本不需要画图,就可以直接计算出公路的半径。如图所示,在这段弧线上取任意两点C和D,并连接点C和点D,测量出CD和EF的长度(EF是弓形CED的高度)。根据这两个数值,就可以计算出圆弧半径的长度。把线段CD和过圆心O的直径看作两条相交的弦,那么:
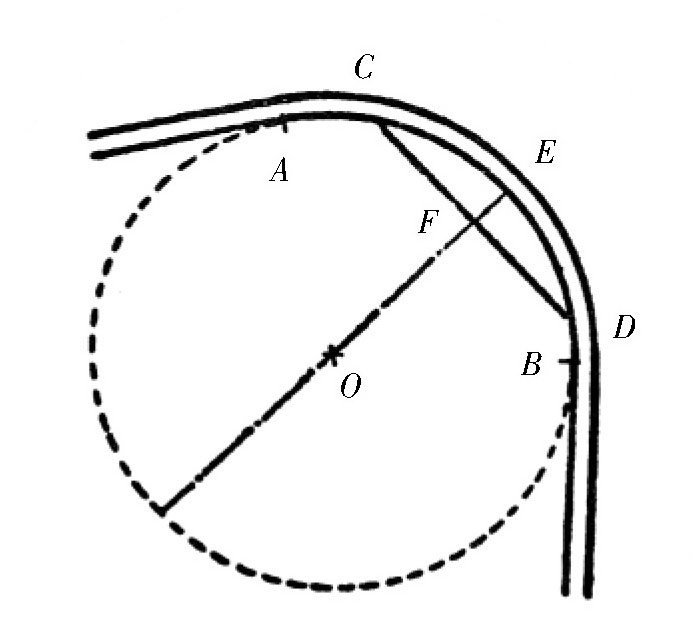
图 公路转弯半径的计算。

这里的a表示弦CD的长,h是EF的长度,也就是弧形CED的高度,R是圆弧的半径。
所以,我们有:
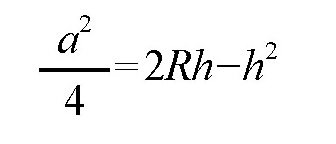
所以,圆弧的半径是:
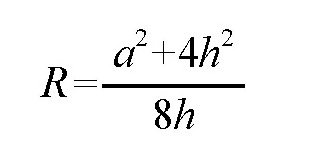
如果h=0.5米,弦CD长48米,那么半径就是:
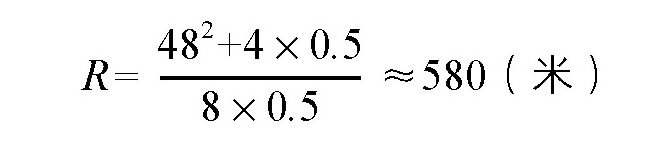
其实,上面的式子还可以简化一下。在实际情况下,h跟R比起来,要小得多。h一般是几米,而R是几百米,所以可以用2R代替2R-h。这样,我们就可以得到一个更简便的计算公式:

如果把刚才的数值代入上面的公式,得到的结果是一样的,也是R≈580米。
得出了曲线的半径,我们就可以知道,这段公路曲线的圆心在弦的中点的垂线上。于是,我们还可以找到这段曲线圆心的位置。
假设这是一段铁路,上面铺有铁轨,那么要计算它的弯路半径,就会变得非常简单。最简单的办法就是,如图所示,找一条绳子,把它拉直,使它跟内侧的铁轨相切,就得到了外侧铁轨的一根弦,h正好是两根铁轨之间的距离。假设两根铁轨之间的距离是1.52米,弦长是a,那么这段曲线的半径就是:

图 铁路转弯处半径的计算方法。
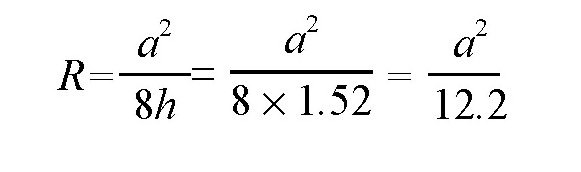
如果a=120,则这段曲线的半径大约是1200米。
其实,在实际生活中,这种方法并不是很实用,绳子要足够长才行。
