如果可能的话,我们把一个物体放到一颗行星内部的最深处,那么,这个物体的重量会发生什么变化?
有的读者可能会不假思索地说:当然变重了,因为这个物体距离行星的中心更近。但这个答案并不正确。实际上,情况正好相反,越到行星的内部,物体所受到的引力不是越大,而是越小。下面,我们就来分析一下。
力学定理和相关计算可以证明,如果把一个物体放在均匀的空心球里,它将不受任何引力的作用,如图所示。同样的道理,如果我们以这个物体到实心球中心的距离为半径、以实心球的中心为圆点画一个球体,那么,这个物体将只受到来自画出的球体中物质的引力,如图所示。
根据上面的分析,我们可以得出一条规律:物体的质量会随着它到行星中心的距离变化而变化。假设行星的半径是R,物体到行星中心的距离为r,如图所示。这时物体会受到两方面的引力:一方面是由于距离缩短使引力变大,将增加到原来的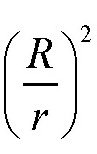
倍;另一方面是由于发挥作用的物质变少使引力变小,将减少到原来的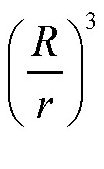
。也就是说,物体受到的总引力是:
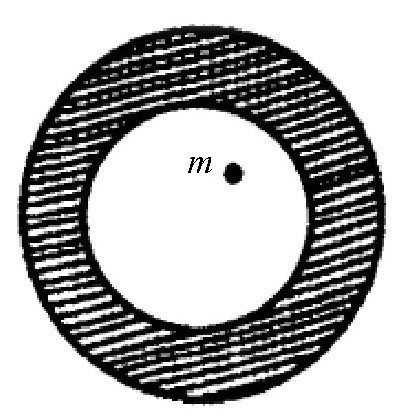
图将一个物体放在一个均匀的空心球里,这个物体不受空心球的引力作用。
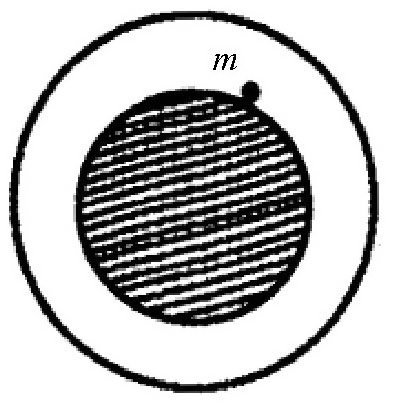
图放入实心球内部的物体所受到的引力,跟图中阴影部分的物质有关。
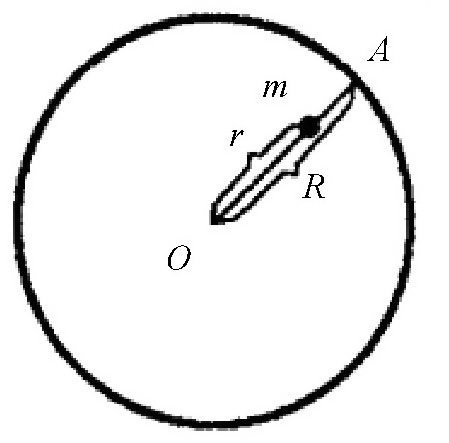
图物体的质量会随着它与行星中心的距离变化而变化。
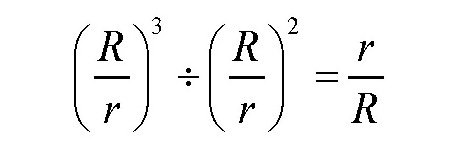
从这个公式可以看出,物体在行星里面的质量与其在行星表面的质量之比,等于物体到行星中心的距离与行星的半径之比。如果这颗行星的大小跟地球差不多,半径也是6400千米,那么,在它里面3200千米的地方,物体的质量将变成原来的1/2;如果物体在行星里面5600千米处,它的质量将变为原来的1/8。
另外,我们还可以得出下面的结论:在行星的中心处,物体的质量将变为0,这是因为:
(6400-6400)÷6400=0
事实上,这一点完全可以通过推理得出。如果物体位于行星的内部,它将同时受到四面八方的引力作用,这些引力由于相互抵消而使得物体的质量也消失了。
需要指出的是,刚才的推理只适用于密度均匀的行星,因为密度均匀是一种理想状态。对于实际中的行星,需要对这个推理进行一些修正。比如地球,它深处的密度比地表的密度大多了,所以,物体所受到的引力随距离变化的规律跟刚才所讲的有所不同。如果物体在距离地面较浅的部分,它所受到的引力将随深度的增加而变大,但是,如果到了地球的深处,这个引力又会越来越小。
