在上一节中,我们得出了一个数字2.7183…,这是一个无理数。在高等数学中,这个数字的作用非常大,通常把它记为e,并用下面的级数来计算它的近似值:
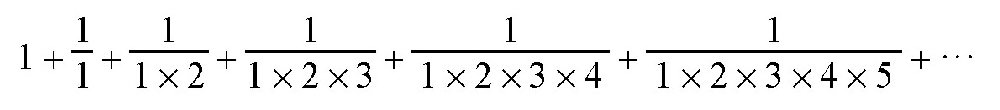
在上节关于存款按复利方式增长的例子中,我们知道e就是式子
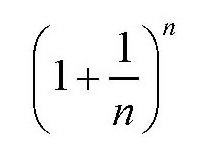
在n趋于无穷大时的极限值。
鉴于很多无法赘述的原因,我们把e作为自然对数的底,这是非常方便的。很早以前就有了自然对数表,并在科学技术中发挥了重要作用。前面的章节中,我们提到了48位、61位、102位,甚至260位的对数“巨人”,它们都是以e作为底的对数。
此外,数e还经常在我们意想不到的地方出现,比如下面的题目:
把数a分成若干份,若使每一份的乘积最大,应该如何分呢?
我们之前已经了解到,如果一组数的和为定值,要想使它们的乘积最大,这组数中的每个数必须相等。很明显,这里的a分成的每一份都相等,那么该分成多少份呢?利用高等数学的知识可以证明:当所分的每份与e最接近的时候,所得的乘积最大。
比如,假设a等于10,该如何分呢?前提是每一份都相等。我们可以先求出e除a的商是多少,它等于

由于不可能把一个数分成3.678…份,所以只能取最接近这个数的整数,也就是4。所以,分成的每一份就是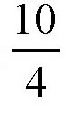
,也就是2.5时,各项乘积最大,这4份的乘积是
2.54=39.0625
可以验证该结论是否正确,如果把10等分成3份或者5份,得到的乘积
将分别是
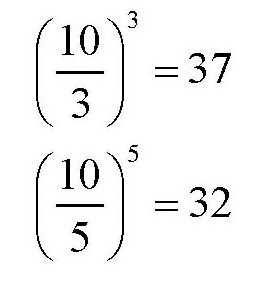
它们都比前面的结果小。
如果a等于20呢?这时,就必须分成相等的7份,因为
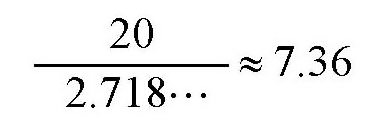
如果a是50,应该分成18份;如果a是100,则应该分成37份。因为
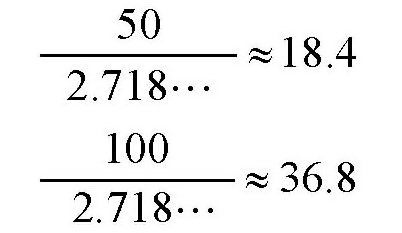
除了在数学领域,在物理学、天文学以及其他的领域中,数e都发挥着非常重要的作用。比如在下面的这些问题中,经常会用到数e:
气压随高度不同而变化的公式,
欧拉公式,
物体的冷却规律,
放射性元素的衰变,
地球的年龄,
摆锤在空气中的摆动,
计算火箭速度的奥尔科夫斯基公式,
线圈中的电磁振荡,
细胞的增殖。
