【题目】如图所示,车工接到一个订单,让他用一个圆锥形材料车出一个圆柱来,要求尽可能地少去掉材料。他思考了很久,都没有确定下来,到底是车成图所示的细长圆柱,还是车成图所示的粗短圆柱?他不知道这两个方案,哪一个合乎要求。读者朋友,你觉得他应该怎样做才能满足条件?

图 车工遇到的难题。
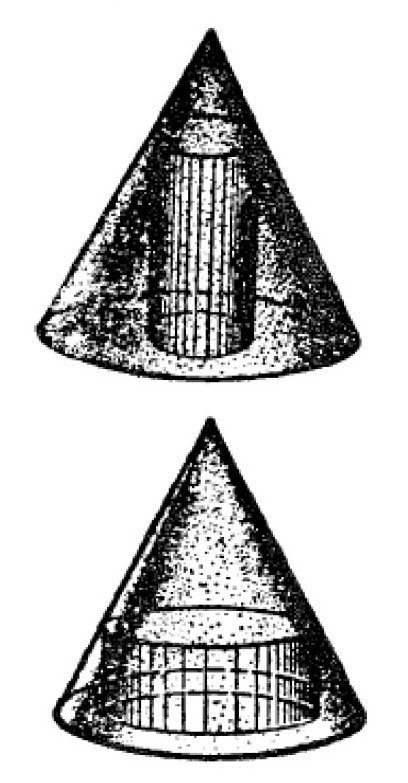
图-186 圆锥中可以车出的两种圆柱,哪个去掉的费料最少?
【解答】说实话,这个题目还是有一定难度的。如 图 所示,我们假设过这个圆锥轴线的截面图为三角形ABC,它的高BD=h,底边半径AD=DC=R。假设图中阴影部分就是我们要车出的那个圆柱的截面,即MNOP,它的顶面跟圆锥顶点的距离BE=x,圆柱的底面(或者顶面)半径PD=ME=r。
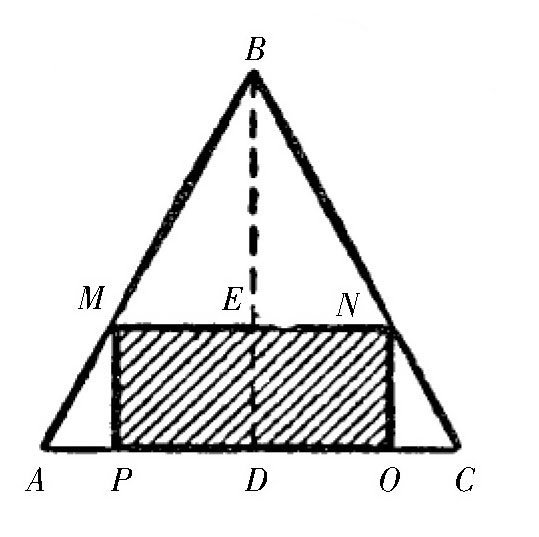
图 圆锥和圆柱通过轴线的截面图。
那么,我们有下面的比例关系:
ME∶AD=BE∶BD
即:
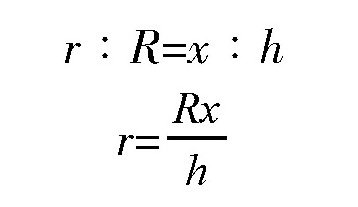
所以,这个圆柱的高就是)h-x),它的体积为:
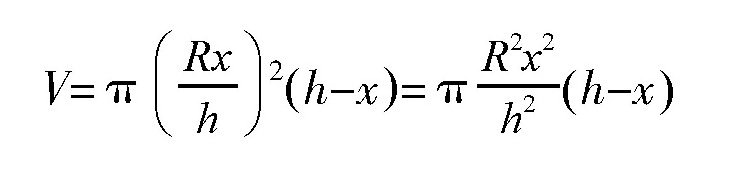
所以可知:
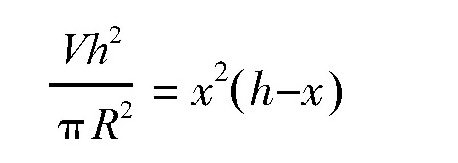
在上式中,左边式子中的h、π、R都是定值,所以要想V最大,就得使右边式子中的x2(h-x )最大。但是,这个式子什么时候最大呢?很显然,右边的式子有三个乘数x、x和(h-x),它们之和并不是一个定值,所以我们需要对它进行一下变换,使这个三个乘数之和为定值。其实,读者朋友应该已经有了答案,就是在前面那个等式的两边都乘以2,即:
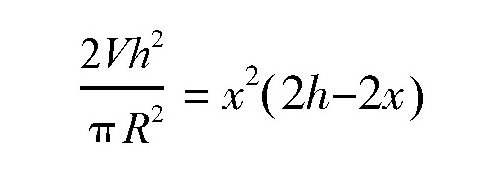
这时候,右边式子中的三个乘数x、x和(2h-2x)之和为:
x+x+(2h-2x)=2h
也就是说,它们的和为定值2h。所以,当这三个乘数相等的时候,它们的乘积最大,也就是:
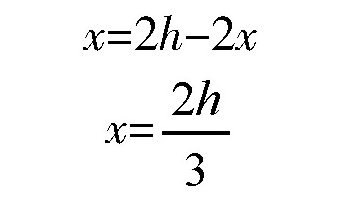
这时,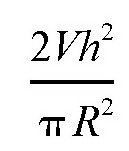
也取得最大值,也就是圆柱的体积V取得最大值。
也就是说,只要圆柱的上底面距离圆锥的顶点为圆柱高度的2/3,就可以得到最大体积的圆柱,这样去掉的材料就是最少的。
