在小学读本中,通常会收入一个故事,是关于一只聪明的乌鸦的。这个故事是这样的:有一只乌鸦,它非常口渴,幸运的它找到了一个细口径的瓶子,但是瓶子里的水不多,乌鸦的嘴又不能伸进瓶子的里面,最后,乌鸦想到了一个办法来解决这个问题,它找了一些小石头,把它们一块一块地扔进瓶子中。结果,瓶子里的水就升了起来,乌鸦喝到了水。
这里,我们不去讨论这只乌鸦是不是真的能这么聪明,我们只对这个故事中的几何学知识感兴趣。我们来看下面的题目。
【题目】假设瓶子里面的水正好到瓶子一半的高度,这只乌鸦能喝到水吗?
【解答】通过解答这个题目,我们就会知道,如果采用乌鸦的方法,并不是任何水量的水都可以喝到。
为了简化问题,我们假设这个瓶子是方柱体的形状,投进去的石头都是大小相同的球体。那么,不难得出,瓶子里水的体积应该大于投进瓶子里的石头空隙的体积。只有这样,瓶子里的水才能升到石头之上。也就是说,水会把石头的空隙全部填满,并且还多余出一部分,可以升到石头上面。
下面,我们就来计算一下,这些空隙究竟占了多大的体积。要想计算空隙的体积,最简单的方法就是假设每块石头的圆心正好在一条竖直线上,也就是说,石头是上下垂直摆放在一条直线上的。假设每块石头的直径为d,那么它的体积就是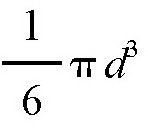
,而跟它外切的立方体体积是d,它们的差就是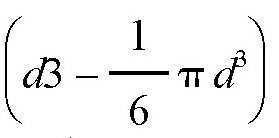
,也就是这个外切立方体中没有被石头占据部分的体积。它们的比值是:
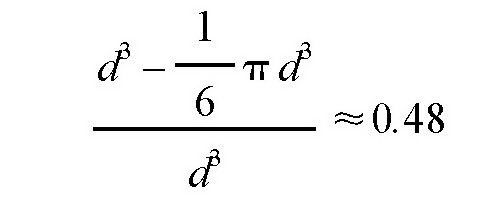
上式的意思就是,在每个外切立方体中,没有被石头占据部分的体积是整个体积的48%。也就是说,瓶子里面所有空隙体积的总和,比瓶子容积的一半稍小一些。如果瓶子的形状不是方柱体的形状,石头也不是球形,答案也不会有丝毫变化。不管在什么情况下,我们可以肯定的一点是,如果瓶子里起初的水量不到瓶子容积的一半,那么不管这只乌鸦怎么往里投掷石头,也不可能使瓶子里面的水升到瓶口的位置。
假设这只乌鸦本领高强,它会摇动瓶子,使里面的石块相互间更紧密,那么,它完全可能把水面提高到原来的2倍高度。但是,这是不可能的,它根本做不到这一点。所以,最实际的情形就是,石头堆积得比较松散,而且,一般来说,盛水的瓶子都是中间比两头要粗一些,这样也会降低水面升高的程度。这样的话,我们几乎可以肯定地说,如果瓶子里面的水不到瓶子一半的高度,乌鸦是无论如何都喝不到里面的水的。
1阿基米德(公元前287~公元前212),古希腊哲学家、数学家、物理学家。
2杰克·伦敦(1876~1916),美国著名现实主义作家,代表作有《马丁·伊登》《野性的呼唤》等。
