【题目】3辆摩托车进行骑行比赛,其中第二辆摩托车的速度比第一辆慢15千米/小时,比第三辆快3千米/小时。三辆摩托车同时发动,已知第二辆到达终点的时间比第一辆晚了12分钟,但比第三辆早了3分钟,而且中途都没有停下来过。
请问:
(1)比赛的全程是多少千米?
(2)每辆摩托车的行驶速度是多少?
(3)每辆摩托车跑完全程花了多长时间?
【解答】初看起来,题目的问题很多,要求的未知数也很多,事实上,我们只要求出其中的两个,就可以得出所有的未知数。
设第二辆摩托车的速度x千米/小时。那么,第一辆摩托车的速度就是(x+15)千米/小时,而第三辆的速度是(x3)千米/小时。
再设比赛的路程全长为y千米,则3辆摩托车跑完全程所花的时间(单位:小时)分别为:
第一辆摩托车: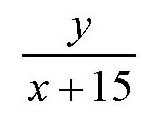
第二辆摩托车: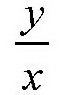
第三辆摩托车: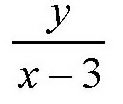
由于第二辆摩托车比第一辆多花了12分钟,也就是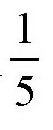
小时。
所以
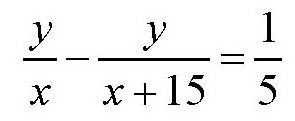
而第三辆摩托车比第二辆多花了3分钟,也就是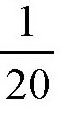
小时,所以
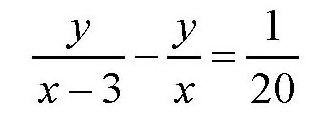
在第二个方程的两边乘以4,然后分别减去第一个方程的两边,可以得到
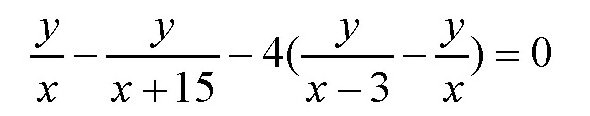
很显然,y≠0,把上面的方程用y除并去分母后,可以得到
(x+15)(x-3)-x(x-3)-4x(x+15)+4(x+15)(x-3)=0
去掉括号,化简可得
3x-225=0
解得
x=75
把x的值代入第一个方程,得到
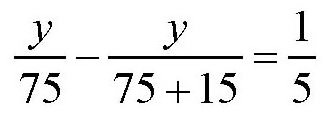
解得
y=90
根据x与y的值,很容易求出这3辆摩托车的速度依次为:90千米/小时,75千米/小时和72千米/小时;而比赛的全程为90千米。
进而可以求出3辆摩托车跑完全程所花的时间依次为:1小时,1小时12分和1小时15分。
