国际象棋棋局共有多少种可能

在本节中，我们就来粗略计算一下，在国际象棋的棋盘上，一共可能会出现多少种不同的棋局。我们只是想让大家知道这个数目会有多大，非常精确的计算没有太大意义，因此我们只是进行一种估算。有一，叫《游戏的数学和数学的游戏》，里面有这样一段文字：

由于白方的每个卒都可以向前走一个格或者两个格，一共有8个卒，共有16种走法；而2个马又分别有2种走法，共有4种走法。所以，白方的第一步一共有16＋4＝20种走法。同样地，黑方的第一步也有20种走法。白、黑两方各走第一步之后，会出现20×20=400种不同的棋局。

走了第一步后，后面的走法就更多了。比如说，如果白子第一步走的是e2-e4，那么，第二步就会有29种走法。再走第三步，可能的走法还会更多。以王后为例，假设它本来在d5格中，且它所有的出路均为空格，那么它可能的走法就有27种。不过，为了计算更简单，我们不妨取它们的平均数：

在双方的前5步中，假设每步的走法都是20种，在以后的每一步中，假设每步的走法是30种。另外，假设在比赛中双方各走了40步。这样，我们就可以计算出，在这盘比赛中，所有可能的棋局数目是

（20×20）⁵×（30×30）³⁵

为求出上式的近似值，我们不妨对上式进行一些变形：

（20×20）⁵×（30×30）³⁵＝20¹⁰×30⁷⁰＝2¹⁰×3⁷⁰×10⁸⁰≈10³×3⁷⁰×10⁸⁰＝10⁸³×3⁷⁰

在上式中，用2¹⁰来代替10³，因为2¹⁰≈1000=10³。

对⁷⁰3可以进行下面的近似：

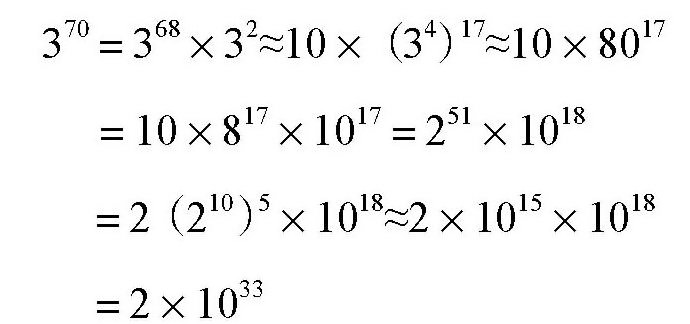
进而

（20×20）⁵×（30×30）³⁵≈10⁸³×2×10³³＝2×10¹¹⁶在传说中，赏给象棋发明人的麦粒数是（2⁶⁴－1），这个数大概是18×10¹⁸，象棋的棋局数可比这个数大多了。假如地球上所有的人每天24小时都在下棋，假设每走一步只需1秒，那么，要想把这些棋局全部实现，所需要的时间大概是10¹⁰⁰个世纪！