几何体的万能公式-辛普森公式

答案是肯定的，确实存在这样的万能公式。这个万能公式的适用范围不仅局限于圆台、圆柱和圆锥，而且对棱台、棱柱和棱锥也适用。这个公式又叫辛普森公式，下面是这个公式的表达式：

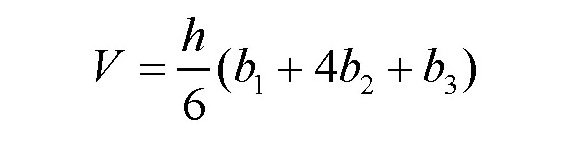
其中，h是几何体的高度，b₁是下底面的面积，b₂是中间截面的面积，b₃是上底面的面积。

【题目】证明辛普森公式可以用于下面的几何体：棱台、棱柱、棱锥、圆台、圆柱、圆锥和球体。

【解答】只要分别利用这个公式来求解一下图所示的几何体的体积就可以了。

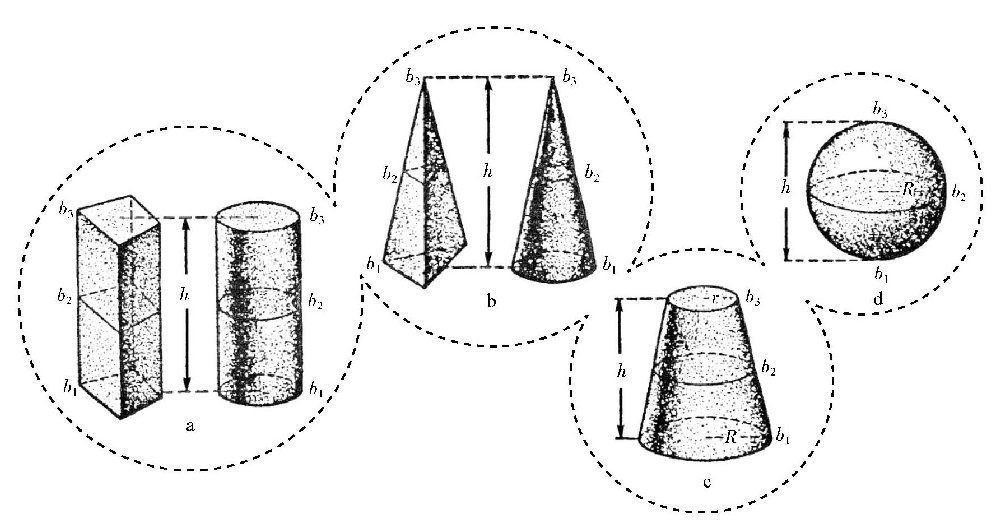
图 万能公式适用的几种几何体。

如果是圆柱或棱柱（如图，a），有：

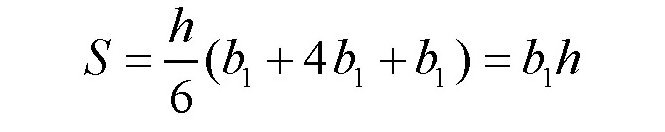
如果是圆锥或棱锥（如图，b），有：

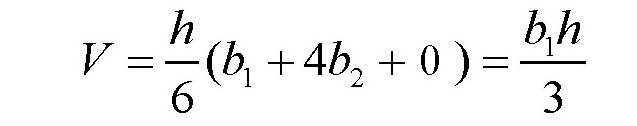
如果是圆台（如图，c），有：

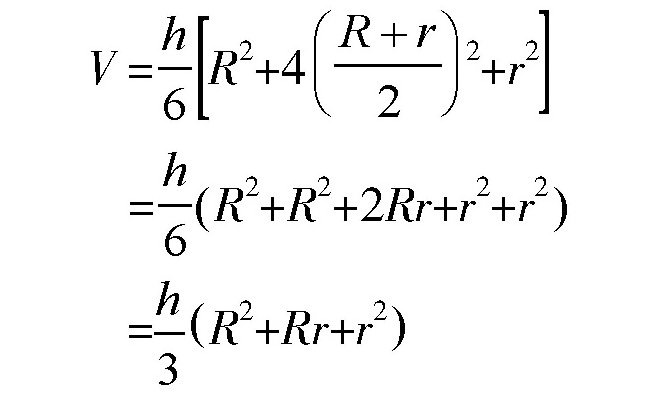
如果是棱台，也可以计算出来。如果是球体（如图，d），有：

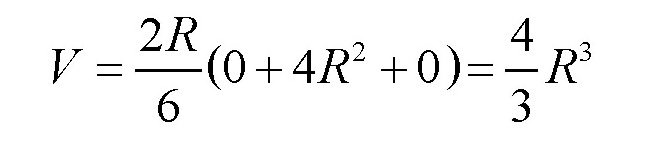
【题目】万能公式还有一个特点，它还可以用来计算平面图形的面积。比如，平行四边形、梯形、三角形等，但是要把公式中字母的含义稍作修改：

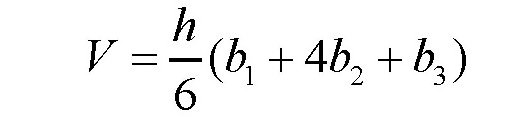
其中，h仍代表高度，b₁是下底边的长，b₂是中间线的长，b₃是上底边的长。

怎么证明呢？

【解答】把公式分别用于三角形、平行四边形、梯形。如图所示。

图 万能公式适用的图形。

如果是平行四边形，有：

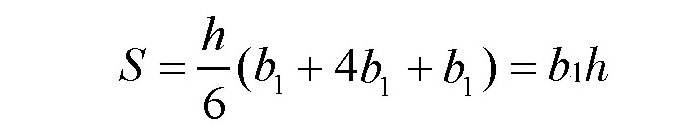
如果是梯形，有：

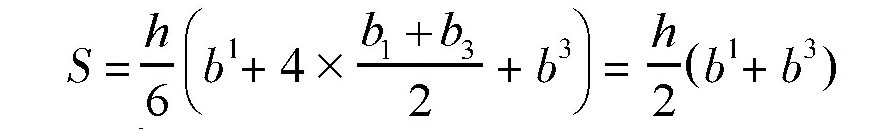
如果是三角形，有：

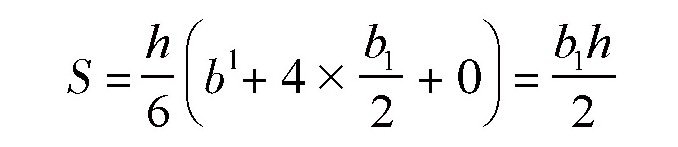
看来，这个万能公式还真是名副其实。