用2累乘的惊人结果,用2累乘1立方米,要累乘多少次才会得到1027立方米?

用2累乘一个很小的数，就可以把这个数变得非常大，而且累乘的次数不需要太多。下面，我们举一个大家不太熟悉的例子。

【题目】草履虫每隔一定的时间就会由一个分裂成两个，这个时间大概是27小时。假设通过这种方法分裂出来的草履虫都能存活，那么，大概需要多长时间，一只草履虫分裂出来的所有后代的体积才能跟太阳的体积一样大？

假设每次分裂的后代都存活，已知一只草履虫分裂40代之后，它所有的子孙所占的体积大概是1立方米，而太阳的体积大概是10²⁷立方米。

【解答】根据已知条件，题目实际上就是问：用2累乘1立方米，要累乘多少次才会得到10²⁷立方米？

我们知道，2¹⁰≈1000，所以10²⁷可以表示成下面的式子：

10²⁷=（10³）⁹≈(2¹⁰)⁹=2⁹⁰

也就是说，在分裂40代的基础上，只要再分裂90次，就可以达到太阳的体积那么大。如果从第一代开始算起，要分裂40+90=130次才能达到太阳那么大的体积。很容易计算出，分裂到130代大概需要147天，过程如下：

27×130＝3510（小时）

3510÷24＝146.25（天）≈147（天）

据说，曾经有一位微生物学家，从草履虫第一次分裂开始观察，一直观察到它分裂了8061次。感兴趣的读者朋友可以自己计算一下，如果这些草履虫一只也没有死掉，经过这么多次分裂以后，所占的体积是多少？

其实，对于这个问题，我们还可以换一种说法：

假设太阳也进行分裂，第一次分裂成两个，每一半又分裂成两个，并一直分裂下去。那么，经过多少次分裂之后，最终形成的粒子和草履虫的体积一样大?

当然，答案也是130次，但是，你可能会觉得不可思议，怎么才这么少的次数？是真的吗？当然是真的。

类似的问题还有很多，比如：把一张纸对半剪开，剪出来的半张纸再对半剪开，这样一直进行下去。那么，剪多少次之后（假设可以一直剪下去），得到的粒子跟原子大小一样?

我们假设一张纸的质量是1克，原子的质量我们取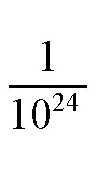

克这

10²⁴=(10³)⁸≈(2¹⁰)⁸=2⁸⁰

所以，一共要剪80次。很多人以为需要剪几百万次，实际上根本没有那么多。