两个农妇共带着100个鸡蛋去集市上卖,虽然她们的鸡蛋数不一样多,但最后却卖了一样多的钱,

在欧拉的著作《代数引论》中，有这样一道题目：

【题目】两个农妇共带着100个鸡蛋去集市上卖。虽然她们的鸡蛋数不一样多，但最后却卖了一样多的钱。一个农妇对另一个农妇说：“如果把你的鸡蛋给我卖，我可以卖15个铜板。”另一个农妇说：“如果把你的鸡蛋给我卖，我只能卖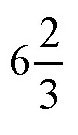

个铜板。”请问，她们分别带了多少个鸡蛋？

【解答】设第一个农妇带了x个鸡蛋，则另一个带了（100-x）个。如果第一个农妇也卖第二个农妇的（100-x）个鸡蛋，她可以卖15个铜板，所以她卖鸡蛋的价格是每个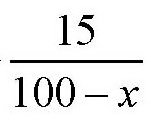

个铜板。

同样的方法，可以得出第二个农妇卖鸡蛋的价格是每个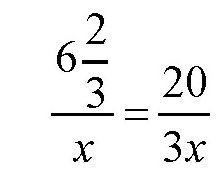

个铜板。

于是，第一个农妇卖得的铜板数为

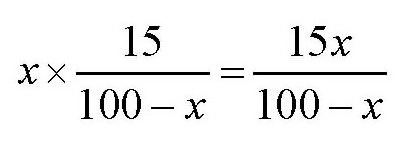
第二个农妇卖得的铜板数为

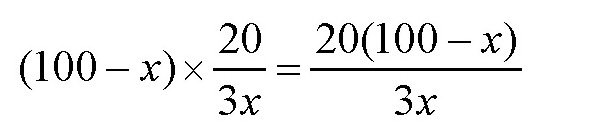
由于她们卖得的钱数相等，所以

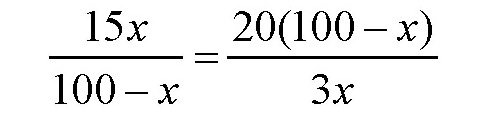
化简可得

x²+160x-8000=0

解方程得

x₁=40,x₂=-200

显然，本题中的负数解没有意义，所以舍去。这样，我们就得到了答案，第一个农妇带了40个鸡蛋，另一个带了60个鸡蛋。

其实，本题还有一个非常简单的解法，但并不是人人都能想到的。

设第二个农妇带的鸡蛋数是第一个的k倍，由于她们卖得的钱数相等，所以第一个农妇卖出每个鸡蛋的价格是第一个的k倍。如果在卖鸡蛋之前，她们把鸡蛋进行了对换，那么第一个农妇手中的鸡蛋数就是第二个农妇的k倍，而她的卖价也是第二个的k倍，所以她卖得的钱数应该是第二个农妇的k²倍，即

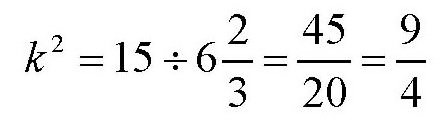
所以

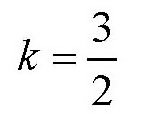
也就是说，第二个农妇的鸡蛋数是第一个农妇的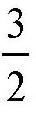

倍，容易得出，第一个农妇带了40个鸡蛋，第二个农妇带了60个鸡蛋。