正方形的特殊性质

在所有周长相等的矩形中，正方形的面积最大，这是正方形的一个特殊性质。其实，很多人并不知道这一点。所以，在这里，我们对这一点进行严格的证明。

我们把矩形的周长记为P，那么，如果这个矩形是正方形，它的边长就是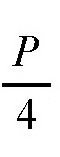

。现在，我们就来证明，如果把其中的一个边长减少b值，同时在另一边加上b值，虽然它的周长还是P，但是面积却比正方形小。也就是说，证明正方形 （边长为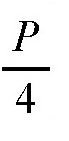

） 的面积比矩形 [边长分别为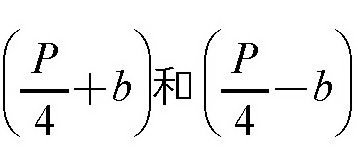

]的面积大，即：

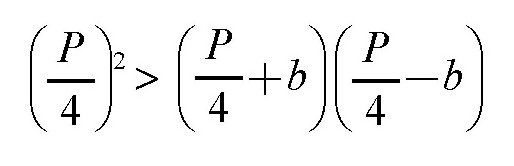
不等式的右边：

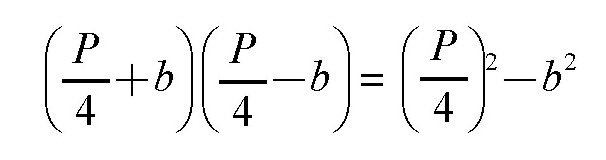
也就是说，上式可以转化成下面的式子：

0＞－b²或者b²＞0

很明显，这个不等式是成立的，这是因为，对于任意的数，它的平方都大于0。所以，前面的那个不等式当然也是正确的。

综上所述，在所有周长相等的矩形中，正方形的面积是最大的。

此外，我们还可以得出这样的结论：在所有相同面积的矩形中，正方形的周长是最短的。下面，我们也来证明一下。

假设上面的结论不正确，也就是说，在面积一定的条件下，正方形的周长并不是最短的。

假设存在这样一个矩形A，它的面积跟正方形B相等，但是周长却比正方形B的周长短。

如果我们用这个矩形A的周长作为一个正方形C的周长，则这个正方形C的面积就会比矩形B大。

正方形C比矩形B的面积大。

正方形C的周长比正方形B小，但是面积却比正方形B大。

这显然是不存在的。

所以说，我们前面的假设是不正确的，并不存在这样一个矩形A，它跟正方形B面积相同，而周长却比较小。因此，我们可以确认在所有面积相等的矩形中，正方形的周长最小。

上文中，如果巴霍姆知道正方形的这两个特殊性质，他完全可以根据自己的体力，获得最大面积的土地。如果他知道自己可以在白天不费力地走出36俄里，他就可以走出一个边长为9俄里的正方形，这样他就可以得到81平方俄里的土地，这比他因过度劳累而死获得的土地还要多出3平方俄里。

反之，如果巴霍姆只想得到一块很小的土地，比如，36平方俄里，他只需要花费很少的体力，走出一个边长为6俄里的正方形就可以了。