有些音乐家也很喜欢数学,虽然他们中的大多数都对数学敬而远之。事实上他们跟数学接触的机会非常多,比他们自己想象得要多得多,而且他们所接触的还不是简单数字,而是比较复杂的对数。
有一位物理学家说过下面一段话:
我有一个喜欢弹钢琴的中学同学,他很讨厌数学。他认为音乐和数学是根本不相通的。他甚至说:“虽然毕达哥拉斯发现了音乐的频率之比,但是毕达哥拉斯的音阶对我们的音乐并不适用。”
可以想见,当我跟他说他每次弹钢琴的时候,实际上弹的都是对数时,这位同学很不愿意承认自己的失败,等音程半音音阶中的每个“音程”,不是根据音的频率,也不是根据波长等距离排列的,而是根据这些数以2为底的对数进行排列的。
假设最低八音度(我们称它为零八音度)的do音每秒振动n次,那么第一八音度的do音每秒会振动2n次,第二八音度每秒振动4n。依此类推,第m八音度的do音每秒振动的次数是n·2m。用p表示钢琴半音音阶中的某一个音调,用0表示每个八音度do。那么sol就是第7个音,la为第9个音,等等。由于在等音程半音音阶中,后面每个音的频率是前面一个音的
倍,所以对于任意一个音的频率,可以表示为下面的公式:

它表示第m个八音度里第p个音的音频。
对上面的式子两边取对数,得

即

假设最低的do音频率为1,即n=1,并把上面所有的对数都看成是以2为底的,即把log2看成1。则上式变为
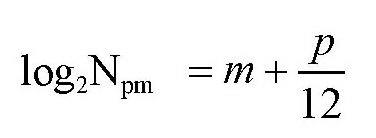
由此可以看出,钢琴键盘上的号码正好等于对应音调频率的对数1其中m是对数的首数,它表示音调位于第几个八音度;p是对数的尾数,它表示音调在该八音度中所占的位置。
以第三个八音度中的sol音为例,它的频率为
,该表达式中的3是这个频率以2为底的对数的首数,而
是这个频率以2为底的对数的尾数。所以,sol音的频率是最低八音度中do音频率的23.583≈11.98倍。
