关于永动机的话题有很多。许多人沉迷其中,有的人最后一无所获,落得悲惨境地。听说有一个人本来生活很富足,为了制造永动机花光了所有的积蓄,最后,永动机没有做成功,他也变成了穷光蛋。从某种意义上说,他只是众多牺牲者中的一个代表而已。后来,听说在他一贫如洗之后,虽然衣不蔽体,仍然没有放弃他所谓的“梦想”,还在找人帮他制造永远也不可能成功的永动机。这听起来很荒谬,也让人感觉很心痛,因为他终其一生都在为不可能实现的理想努力。归根结底,这是因为他连物理学的基本常识都不懂,一直在用错误的理论指导实践。
但是,我们也不得不承认,虽然永动机不可能实现,但是人们在发明永动机的过程中,有很多有趣的新发现。
16世纪末到17世纪初,荷兰有一位数学家非常著名,他叫斯台文,就是在对永动机理论进行深入分析后,提出了斜面上的力量平衡定律。不仅如此,这位著名的数学家还发明了很多其他的理论,一直到现在,对我们的生产生活都产生着重大的影响,比如说小数,就是他发明的。并且在代数学中,首次提出指数的概念。流体力学定律也是他发明的。后来,帕斯卡对这一定律进行了重新论证。
斯台文在提出斜面上的力量平衡定律的时候,没有用到我们常说的平行四边形法则,而是利用了图所示的模型。从图中可以看出,三棱体一共挂着14个小球,每个大小都一样。奇怪的是,这一串小球保持了平衡,并没有滑动。下面的小球不会滑动,这很容易理解,那右边的两个球和左边的四个球呢,也能保持平衡吗?我们说,当然可以,它们也能保持平衡,否则,整串小球就会不停地滑动,因为只要有一个小球动了,其他的也会跟着动,因为它们是串在一起的。前面已经说了,所有的小球并不会滑动。所以我们说,这串小球不会滑动,也就是说,右边的两个小球和左边的四个小球拉力相等,保持了平衡——是不是很神奇?
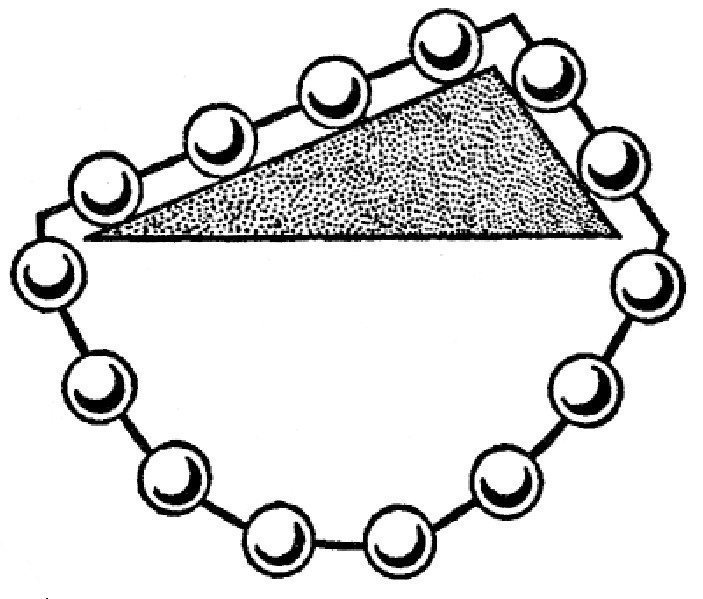
图 斯台文永动机。
通过这一不经意的发现,斯台文提出了斜面上的力量平衡定律。通过观察,斯台文发现,两个斜面上的小球重量的比值,正好是两个斜面长度的比值,并由此得出了结论。也就是我们现在所知道的斜面上的力量平衡定律:
如果两个物体连在一起,放到两个斜面上,要想达到平衡,物体重量的比值必须与两个斜面长度的比值成正比。
由此,还可以推论得出另一个定律,就是把其中的一个斜面换成垂直面。如果想要斜面上的物体保持平衡,必须在垂直面的方向上向下施加一个力,这个力的大小和斜面上物体重量的比值,等于垂直面的长度与斜面长度的比值。
由此可以看出,在发明永动机的过程中,人们阴差阳错地发现了很多有意义的力学理论。
