画中的难题

如图所示，这是波格丹诺夫-别尔斯基的一幅名画，名字叫《口算》，有的读者可能知道它。但是，看过这幅画的人并不一定深入了解图中的“难题”。这个所谓的“难题”就是要人们利用口算很快算出下面式子的值：

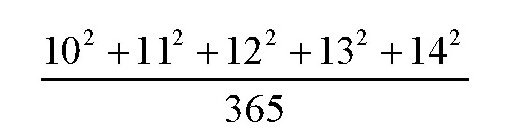
这个题目看上去并不容易解答。但是，对于画中的老师拉金斯基所教的学生来说，这个题目并不难。拉金斯基是一位自然科学领域的教授，他放弃了大学教授的职位，自愿到乡村当了一名普通的数学教师。他在学校的时候学习过口算，对于数的性质很了解。他发现，10，11，12，13，14有下面的特性：

10²+11²+12²=13²+14²

而10²+11²+12²=365，所以，对于前面的分式，可以很容易得出答案，结果等于2。

正是代数方法，可以使我们对数的一些有趣特性得以推广。读者可能会有这样的疑问：除了前面的5个数字，还有没有别的连续整数，也满足这一特性？

【解答】不妨假设这种可能是存在的，并且设其中的一个数为x，那么，可以列出下面的方程：

x²+(x+1)²+(x+2)²=(x+3)²+(x+4)²

这个方程求解起来不是很方便。所以不妨设第二个数为x，于是得到方程：

(x-1)²+x²+(x+1)²=(x+2)²+(x+3)²

化简可得

x²-10x-11=0

解方程得

x₁=11,x₂=1

也就是说，满足这一条件的数有两组，分别是

10，11，12，13，14

和

－2，－1，0，1，2

事实上，

(-2)²+(-1)²+0²=1²+2²

所以，这组数也满足题目的要求。