前面的题目都是只利用直尺而不使用圆规来作图就可以解答的。现在,我们来看另外几个题目,这里的限制条件跟上面的正好相反,要求只许使用圆规,而不能使用直尺作答。说到这类题目,曾经让拿破仑也很感兴趣。据说,他在读了意大利学者马克罗尼关于这类题目的著作后,给数学家们出了这样一个题目。
【题目】不使用直尺,把一个已知圆心的圆周平均分成四部分。
【解答】如 图 所示,假设圆O是题目给出的。现在,要求把它的圆周平均分成四部分。
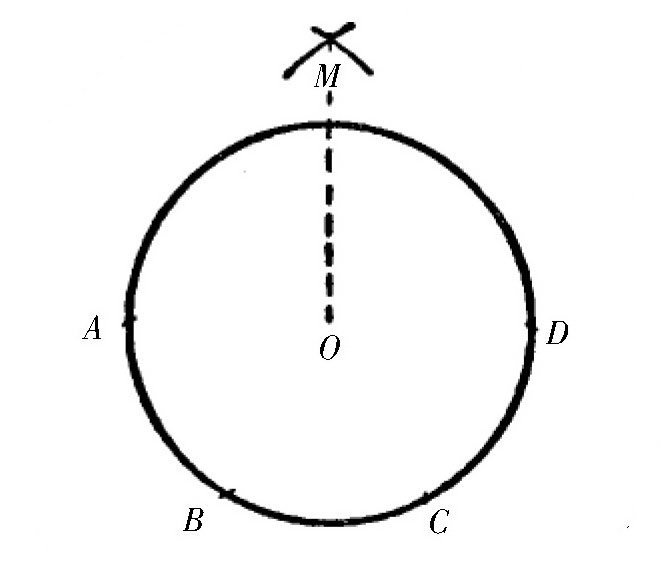
图 仅使用圆规,你能将圆周四等分吗?
把圆规的两只脚放到圆心和圆上的一点,测量出它的半径r。然后,保持圆规的两只脚不动,从圆周上的点A开始,在圆周上依次作出点B、点C和点D。那么,根据圆的性质,我们可以得出,弧线AC的长度等于圆周长度的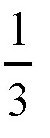
,也就是说,AC是这个圆的内接正三角形的一条边,所以它的长度是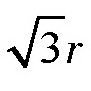
。而AD的距离正好是圆的直径,也就是2r。接下来,以AC为半径,从点A和点D分别画一条弧线,相交于点M,那么MO间的距离正好是这个圆的内接正方形的边长。为什么呢?
三角形AMO的直角边
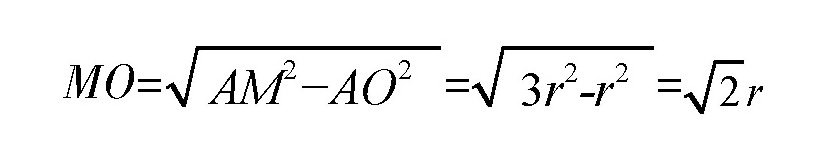
这个长度正好是这个圆的内接正方形的边长。
接下来,只要以MO的长度为半径,用圆规在这个圆周上划分,就可以画出这个圆的内接正方形的顶点。很明显,这些顶点正好把圆周平均分成了四部分。
下面,我们再来看一个更简单的题目。
【题目】如 图 所示,不使用直尺,使点A和点B之间的距离增加到5倍,或者其他任何的倍数。
【解答】在图中,以AB为半径,点B为圆心,用圆规画一个圆。从点A开始,以AB为长度,在画出的圆周上依次画三个点,找到点C,那么点C和点A的连线必过圆心B。也就是说,AC是圆的直径,所以AC=2AB。
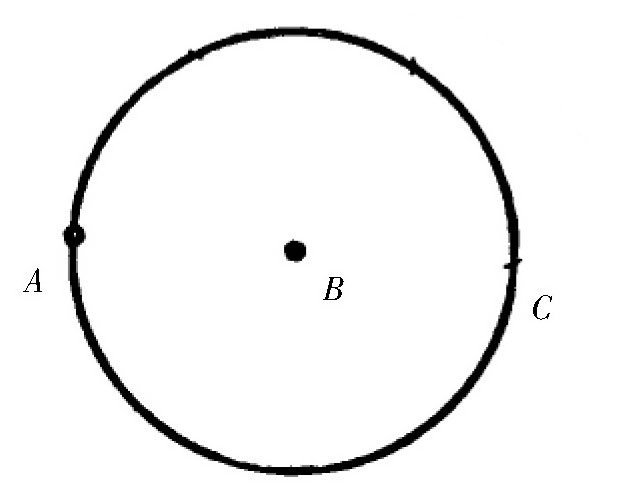
图 只使用圆规,你能将A、B两点间的距离增加n(整数)倍吗?
然后,再以BC为半径,点C为圆心画一个圆,可以得出这个圆上与点B相对的直径上的一点。也就是说,这个点到点A的距离等于AB的3倍。后面的步骤就很简单了,读者朋友可以自己试一下。
