我们知道,地球上的每一个物体,都受到地心引力的作用。如果把物体抬高,地心引力就会减小。比如,把一个1千克重的砝码拿到离地面6400千米的高度,也就是说,砝码离地球中心的距离是地球半径的两倍,那么这个砝码和地球之间的引力只有在地面时的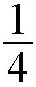
。从另一个角度来讲,如果在6400千米的高空称这个1千克的砝码,它的重量只有0.25千克。根据万有引力定律,计算地球和物体之间的万有引力,常把地球的质量集中在地心位置,万有引力与距离的平方成反比。刚才的这个例子,砝码离地心的距离是地球半径的两倍时,万有引力就是原来的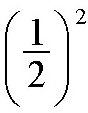
,也就是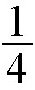
。如果把砝码拿到离地面12800千米的高空,也就是说,砝码离地心的距离是地球半径的3倍,此时万有引力就只有原来的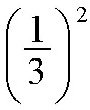
,也就是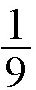
,在这个高度称这个砝码,重量只有111克。
那么,是不是说,物体离地心越近,它受到的引力就会越大呢?还是以砝码为例,如果真是这样,那么砝码在地下越深,它的重量就越重。但是很遗憾,这个推论是错误的。相反,物体在地下越深,它的重量不是变大,而是变小。该怎么解释这一现象呢?
是这样的:如图所示,在地面以下,对物体产生引力的物质微粒把物体包裹在其中,而不是在物体的某一方向。从图中我们看到,在地面以下的砝码,受到两个力的作用,一个是砝码下部的地球微粒对它的吸引,一个是砝码上部的地球微粒的吸引。
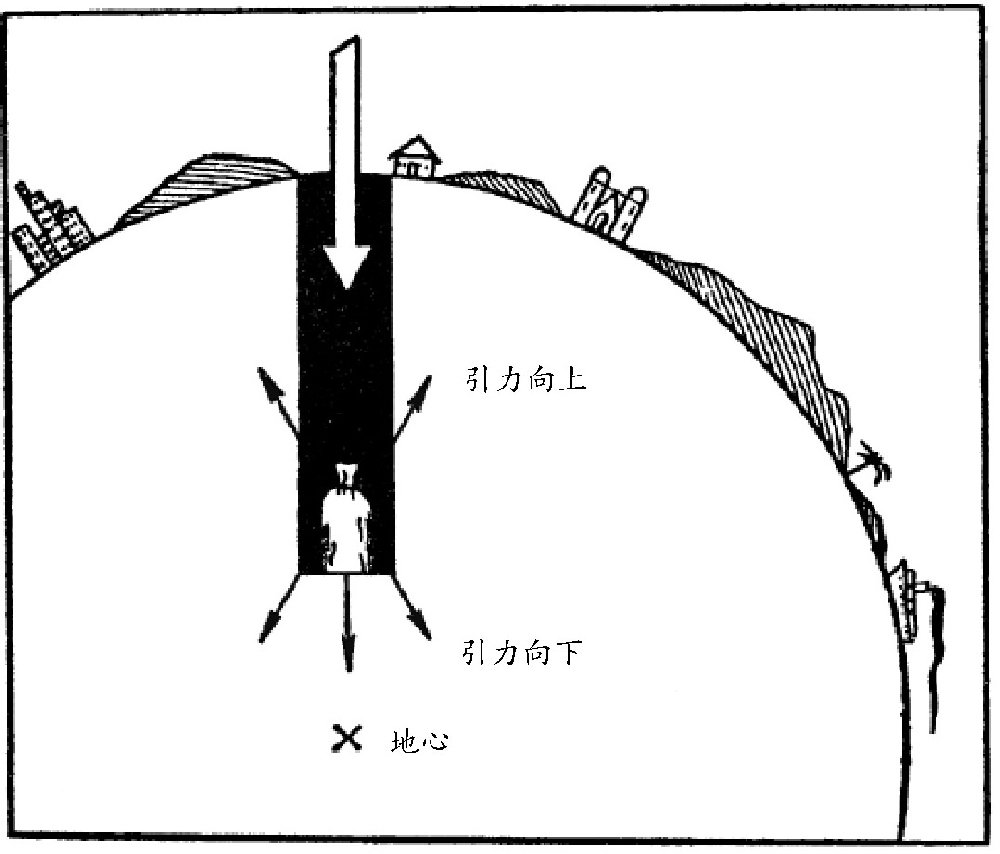
图 在地面以下,砝码的受力分析图示。
需要注意的是,对于地面以下的物体而言,真正作用在它身上的引力,只有物体下面的球体,这个球体的半径就是这个物体和地心之间的距离。所以,物体离地心越近,它的重量会迅速减小。如果物体在地心,四周的地球微粒对物体产生的引力完全相等,物体的重量就会完全失去,变成一个没有任何重量的物体。
因此,可以说,物体在地面上的重量是最大的,在高空或深入地下,它的重量就会小得多(这里,我们假定地球的密度是相等的。其实,实际情况并非如此,越靠近地心的地方,密度越大,所以物体在深入地下的时候,一开始的重量是增加的,到了一定值后才会变小)。
