关于水槽的题目,大家都非常熟悉,几乎每一本算术或者代数习题集都会把这个类型的题目收录进去。对于这样一类经典但非常枯燥的习题,读者们或许还有些印象:
一个水槽里有两根水管(如图)。用第一根管子把水槽装满,所需要的时间是5个小时,用第二根管子把水槽的水放空需要的时间是10个小时。如果同时打开两根管子,要想把空水槽装满水,需要多少小时?
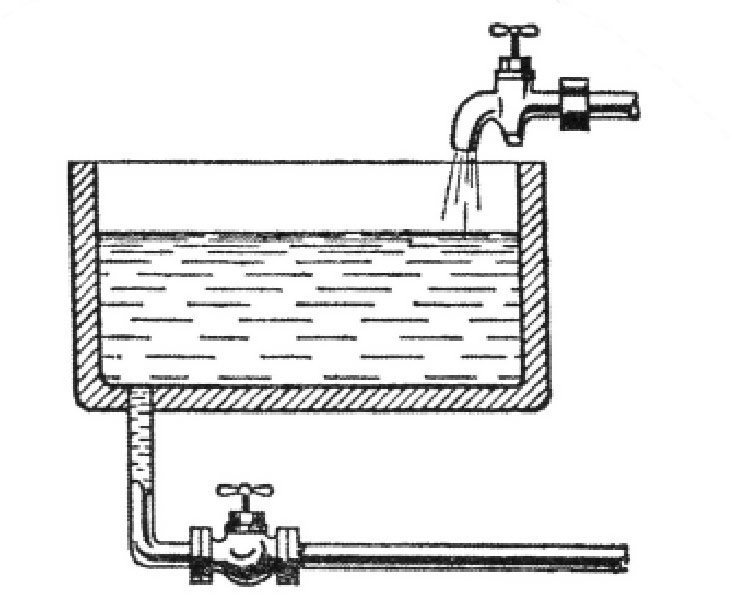
图 “水槽问题”图示。
这个题目可以追溯到亚历山大时期的希罗时代,距今至少已经有20个世纪了。下面就是希罗提出的一个类似题目,与后世的问题相比,他的问题要简单多了:
一个大水池里有4个喷泉:要想把水池灌满,第一个喷泉需要一昼夜的时间;第二个喷泉需要两天两夜的时间;第三个喷泉的能力只是第一个喷泉的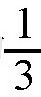
;最后一个喷泉更慢,它需要4个星期才能把水池灌满。那么,请告诉我:如果4个喷泉同时工作,需要多长的时间可以把水池装满?
2000年来,人们一直都在解答关于水槽的同类问题。可2000年来,人们的解答思路都是错误的。可见墨守成规的力量有多大!上一节所讲的关于水流问题的内容如果你弄明白了,就知道人们为什么会解答错了。
人们一般是怎么解答水槽问题的呢?对第一个问题,解答方法一般是这样的:
第一根管子在1个小时的时间内能把水槽灌满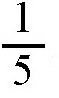
。同时,水被第二根管子抽走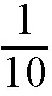
。也就是说,如果两根管子同时打开,每小时灌进水槽的水就是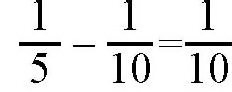
。所以,10个小时就能把水槽灌满。其实,这种推理是错误的。如果进水时因为水流是均匀的,所以进水时受到的压力相同,那么在出水的时候,因为水面在不断升高,压力发生变化,所以水流就不再是均匀流出的了。因此,我们根本不能下结论说,第二根水管需要10个小时抽完水,那每小时就有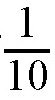
水槽的水流出。由此可见,运用中学学到的数学知识来解答这个问题是不对的。由于涉及水往外流时速度发生了变化的问题,初等数学是解答不了这个问题的,所以算术习题集里根本就不应该收录这类习题。
