对于上文中所提到的各种计算,一定会有一些读者朋友愿意自己来验证。在这里,我们把这些算法都列出来。不过,这些数值只是近似数值,因为我们假定炮弹在炮膛里是均匀加速的(实际上不同时刻的加速度并不同)。几道关于
在后面的计算中会用到以下公式:
t秒末的速度为:v=at。(其中,a为加速度。)
t秒内经过的距离为: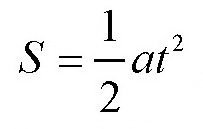
。
根据这两个公式,我们可以先计算出在哥伦比亚号大炮炮膛里时,炮弹的加速度是多少。小说里说没有装火药的炮膛部分长是210米。这也就是大炮需要走的路程S。
上文中已介绍炮弹最终的速度是:v=16000米/秒。在知道了S和v之后,假设炮弹进行的是匀加速运动,那么我们就可以计算出炮弹在炮膛里运动了多长时间。由于 V=at=16000,代入公式可得:

可得:
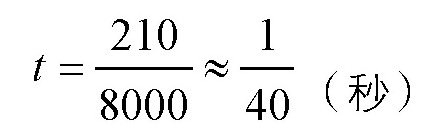
炮弹在炮膛里差不多滑行了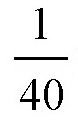
秒,把数据代入公式v=at,可以得出:
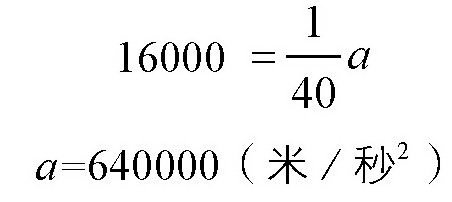
也就是说,炮弹在炮膛里的加速度是640000米/秒2,这几乎是重力加速度(g)的64000倍。如果只想让炮弹的加速度是重力加速度的10倍,也就是100米/秒2的话,炮膛需要有多长呢?
把刚才的算法进行逆运算就可以得到:已知数据a=100米/秒2,v=11000米/秒(在真空中运行,没有大气阻力时,能达到这样的速度)。
由公式v=at,代入数据,可以得到:
11000=100t
t=110(秒)
通过公式
,可以算出炮膛的长度,代入数据可得:
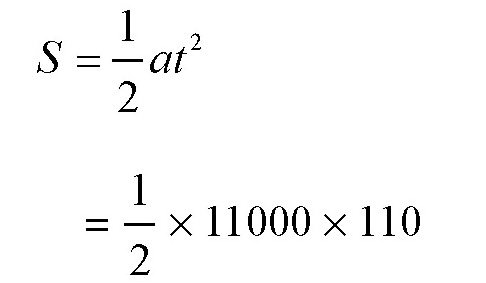
S取整可得600米。
这些数据可以轻松驳倒凡尔纳小说中看似非常诱人的计划了。
