朋友们,给你一把扫帚,如果把它拆开,你可以很容易地把每一根枝条折断。但是,在系好的情况下,你是否还能折断它?
——绥拉菲莫维奇《在晚上》
很多读者可能都听过7根树枝的古老寓言。寓言中,父亲为了让儿子们能够和睦生活下去,把7根树枝系在一起,让他们把这束树枝折断。儿子们轮流进行了尝试,结果都没有成功。最后,父亲把这束树枝拆了开来,然后再一根根折断,很容易就成功了。
这个寓言中包含着力学原理,即强度。下面,我们就来研究一下这个原理。
如图所示,在力学中,杆的弯曲程度通常用挠度 x 来表示。杆的挠度越大,它就越容易被折断。挠度的大小通常用下面的公式来表示:
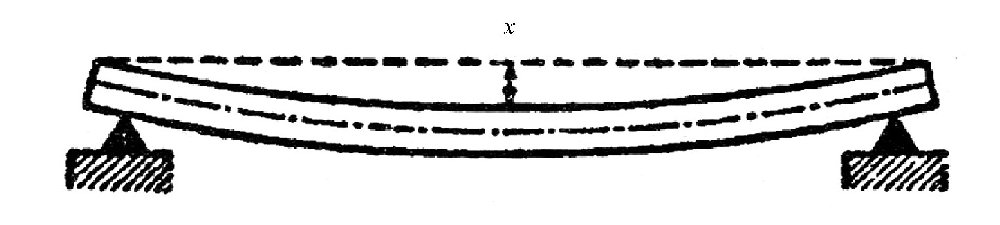
图 挠度 x 示意图。
挠度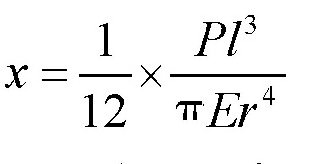
其中,P表示作用于杆上的力、l表示杆的长度、π是圆周率、E表示杆的材料的弹性、r表示杆的半径。
我们可以运用这个公式来分析前面的寓言故事。如 图 所示,假设这7根树枝的位置是按照图中的样子放置的,图中画出的是这束树枝的端面。如果树枝扎得非常紧,我们就可以把这束树枝看作一根实心杆,虽然中间总是有一些空隙,但并不影响我们的分析。从图中可以看出,这根实心杆的直径大概等于一根树枝的3倍。通过下面的分析,我们就可以知道:弯曲(或者折断)一根树枝,比弯曲(或者折断)这根实心杆要容易很多倍。假设需要作用在一根树枝上的力为p,而作用在7根树枝扎成的实心杆上的力为P,那么p与P之间的关系就可以通过下面的式子来计算:
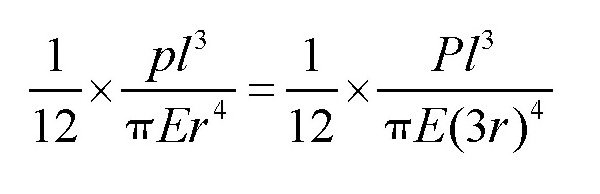
可得:
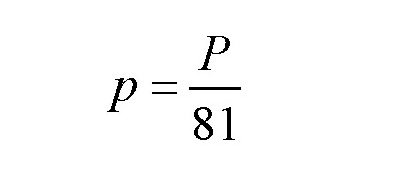
可见,折断一根树枝所需要的力只有折断整束树枝的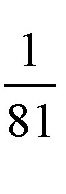
。
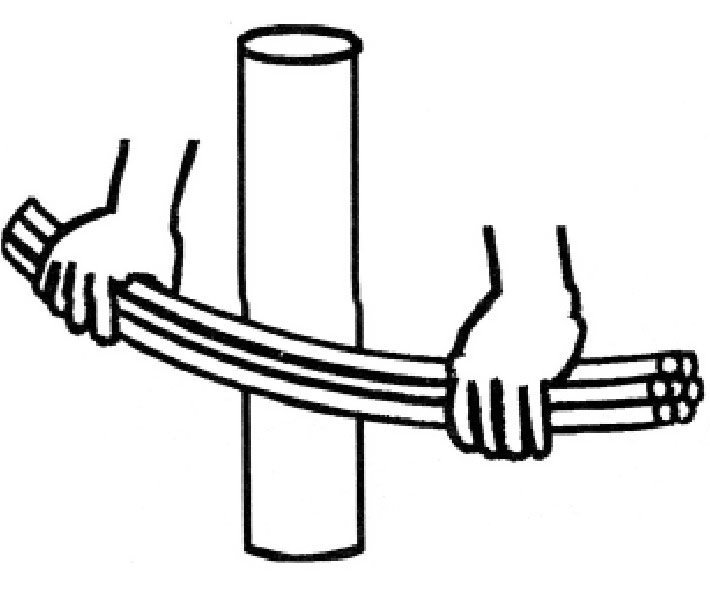
图 扎得很紧的7根树枝。
