【题目】如 图 所示,这位铁匠接到了一个订单,求用一块边长为60厘米的正方形铁皮做一个盒子,不需要做盒盖,但是盒底必须是正方形,而且要求容量达到最大。这可难住了这位铁匠,他思考了很久,不停地拿着直尺量这块铁皮,最终也没有想出来应该怎么做。读者朋友们,你可以帮他一下吗?

图 182铁匠的难题。
【解答】如 图 所示,我们假设这块铁皮的每条边都应该折进去x厘米,则盒子的底边长度为)60-2x)厘米,那么,盒子的容量V就可以表示成下面的式子:
V=(60-2x)(60-2x)x
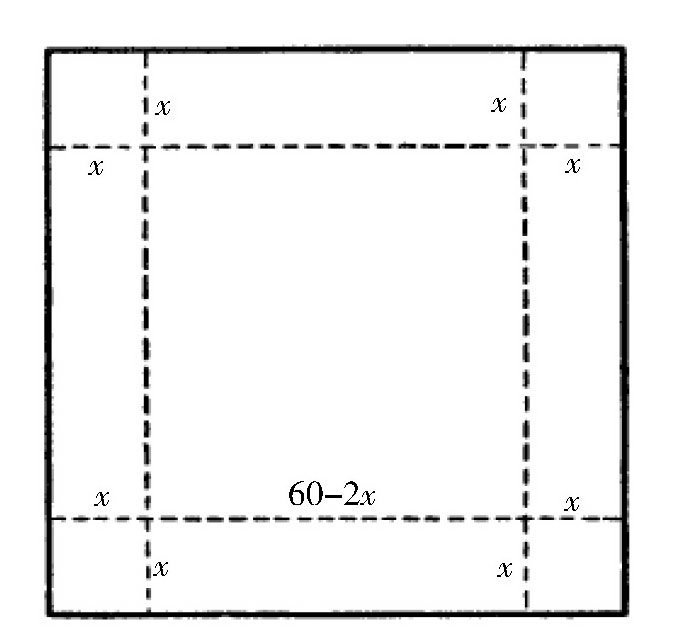
图 铁匠的解答方法图示。
在右边的式子中有3个乘数。如果这3个乘数之和为定值,那么当这3个乘数相等的时候,它们的乘积最大,也就是盒子的容量V最大。下面,我们来看看这3个乘数的和是多少:
(60-2x)+(60-2x)+x=120-3x
也就是说,它们的和并不是一个定值,会随着x的变化而变化。但是,我们可以将前面的等式变化一下,在两边都乘以4,得到:
4V=(60-2x))60-2x)4x
右边3个乘数之和就变成了定值:
(60-2x)+(60-2x)+4x=120
此时,当这三个乘数相等的时候,它们的乘积最大,即:
60-2x=4x
所以:
x=10
这时候,盒子的容量V取得最大值。
因此,只要把这块铁皮从每边折进10厘米,做成的盒子的容量就是最大的。我们还可以计算出这个容量的大小,就是:
40×40×10=16000(立方厘米)
如果铁匠不是这么折的话,哪怕他多折或者少折1厘米,得到的盒子的容量都比这个小。我们可以计算一下,看看是不是这样。
多折1厘米时,容量为11×38×38=15884立方厘米。
少折1厘米时,容量为9×42×42=15876立方厘米。
显然,跟16000立方厘米相比,它们要小一些。
