关于这个问题,我们可以利用前面的计算铁路转弯半径的公式来解答。
实际上,在刚才的题目中,我们已经得到了准确的答案:“水山”是存在的。只不过,这里的“存在”,是几何学上的解释,而不是物理学上的概念。每一片海洋、每一个湖泊,从某种程度上说,都是一座“水山”。当我们站在水边的时候,在我们跟对岸的某一点间,水面是凸起的,而且湖面越宽,凸起的程度就越明显。我们甚至可以求出这个凸起面的高度:
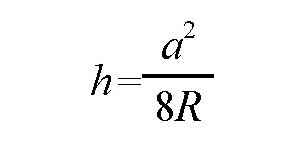
公式中,a是两岸的直线距离,我们可以用湖的宽度来代替。假定湖的宽度是100千米,那么这座“水山”的高度就是:
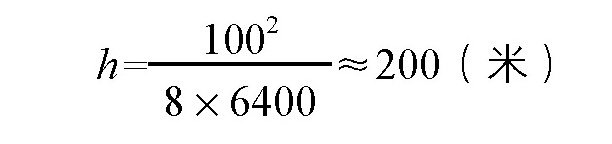
这座“山”还真高呢!
即便湖的宽度只有10千米,跟两岸间的直线相比,它的“山峰”也有2米多高,比一个普通人的身高还要高出不少。
那么,我们可不可以把凸起的水面叫“水山”呢?
如果从物理学上来说,当然是不可以的,因为它并没有高出水平面,那里还是一片“平原”。如图所示,如果把两岸间的直线AB看成是水平的,而把ACB看成是高出水平面的弧线,这是不正确的。其实,这里的水平线不是AB,而是ACB,也就是说,我们以为的直线ADB实际上是凹下去的,AD是向下倾斜的,到了D又向上升起到B,D是AB的最低点。如果沿着AB修一条管子,并在点A放一个铁球,那么,由于惯性作用,球会滚到点B,到了点B后并不会停住,而是返回来,经过点D,到达点A,并不停地滑来滑去。如果管子的内壁足够光滑,铁球跟管子之间没有摩擦力,管子里也没有任何空气,那么铁球就会在点A和点B之间永远滚下去。
所以说,虽然从几何学来说,ACB是一座“山”,但是从物理学来说,它只是一块“平地”。

图 “水山”。
1亚历山大·谢尔盖耶维奇·普希金(1799~1837),俄国著名诗人、作家,被称为“俄国文学之父”,代表作有《叶甫根尼·奥涅金》《上尉的女儿》等。
