现在,我们来讲一个近似解方圆问题的方法。这种方法是由俄罗斯工程师宾科提出的。因此在此方法中用到的三角板也被称为“宾科三角板”。在实际生活中,这个方法使用起来非常方便。
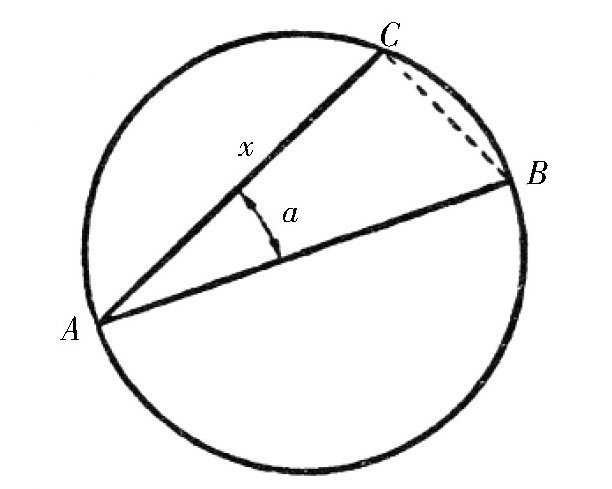
图 解方圆问题的近似方法。
方法是这样的:如图所示,作出一个角α,使它满足下面的关系:
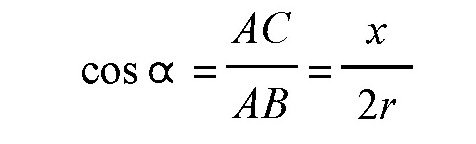
这里的AB是圆的直径,r是半径。AC=x是圆上的一条弦,也是所求的正方形的边长。我们知道cosα是α的余弦函数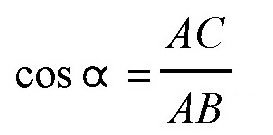
也就是说,正方形的边长x为2rcosα,它的面积是4r2cos2α。从另一种意义上说,正方形的面积是πr2,也就是这个圆的面积。所以:
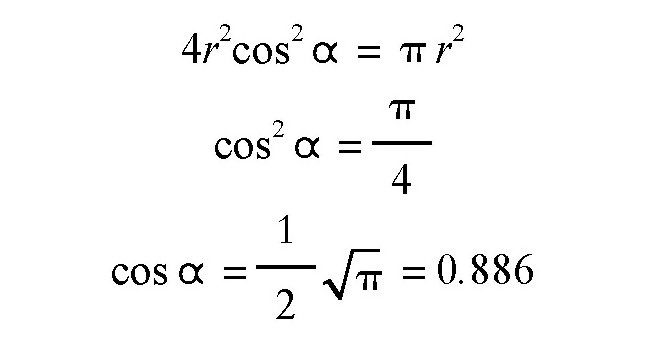
通过查阅三角函数表,我们得到:
α=27°36′
所以,只要作一个弦,使它和直径成的角是27°36′,我们就得到了这个正方形的边长,这个正方形的面积也等于圆的面积。在实际中,我们可以做一块三角板,使它的角度为27°36′。有了这块三角板,我们就可以对任何一个圆,作出一个和它等面积的正方形。
如果你真的想自己制作一块这样的三角板,下面的内容可能会帮到你。
27°36′的正切函数,也就是tan27°36′,它的值是0.523,或者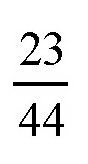
。也就是说,三角形的两条直角边的比值是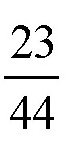
。
所以,在制作的时候,你可以这样做:先作一个直角三角形,然后把一个直角边的长度取22厘米,另一直角边的长度取11.5厘米,这样就可以得出这个角度了。当然,利用这块三角板,我们也可以作出其他的图形。
