【题目】如图所示,这是一个湖,在点C处用指南针测得的数据是这样的:直线CA在SN偏西21°,直线CB在SN偏东22°,而AC=35米,BC=68米,那么,湖水的宽度AB是多少呢?
【解答】在三角形ABC中,角ACB=43°(21°+22°),AC=35米,BC=68米,作AD垂直于BC,则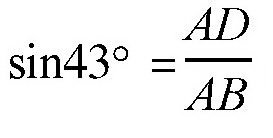
,而sin43°=0.68,所以:
AD=0.68×AC≈24
根据勾股定理,我们有:
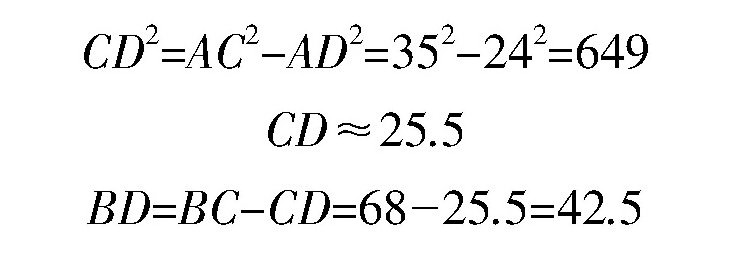
在三角形ABD中,由勾股定理,有
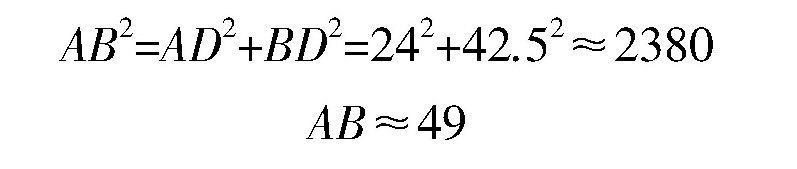
湖水的宽度大概是49米。
如果还要求计算三角形ABC另外两个内角的大小,可以在求出AB的值后,按下面的方法计算:

图 湖宽的测算方法。
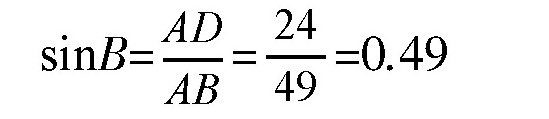
根据前面的方法,得出角B=29°。
根据三角形内角和等于180°,可以得出角A的大小:
∠A=180°-29°-43°=108°
有时候,在三角形的求解中可能会遇到内角大于90°的情况,也就是钝角,这时该怎么求解呢?如图所示,角A是一个钝角,已知它的大小和与它相邻两边的长度,要求计算出另一边的长度和其他两个内角的大小。其实,这个问题的计算方法跟前面的方法是一样的,只不过这里作的垂线BD在三角形的外面,也就是在CA的延长线上,利用三角形BDA,求出BD和AD的大小,那么DC=DA+AC,DC的大小就知道了,BC也就求出来了,而
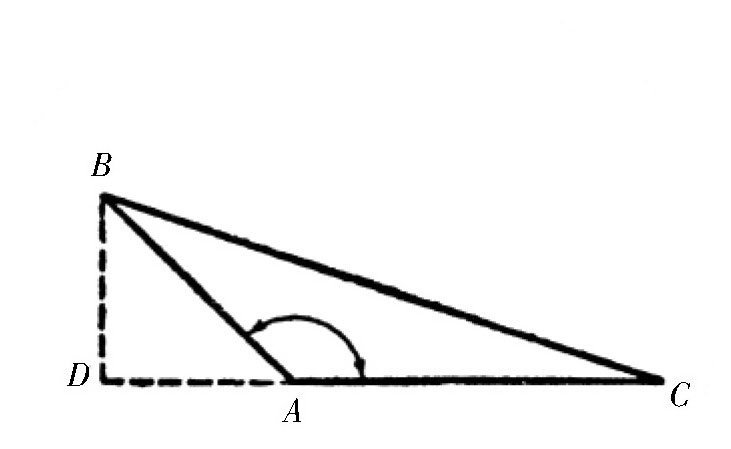
图 钝角三角形的解法。
