第六种运算-开方

对于加法和乘法来说，分别只有一种逆运算，即减法和除法。但是对于第五种运算乘方，却有两种逆运算：求底数和求指数。我们把求底数称为第六种运算，也叫开方；把求指数称为第七种运算，也叫对数。那么，为什么乘方的逆运算有两种，而加法和乘法的逆运算只有一种呢？这是因为，加法中两个数的位置是可以互换的，乘法也是一样。但是乘方的底数和指数是不能互换的，比如，5³3≠5³。所以，对于加法和乘法来说，可以用同样的方法求出这两个加数或者乘数，但是乘方的底数和指数的求法是不一样的。

对于第六种运算——开方，我们用符号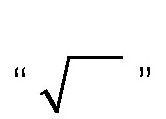

表示。为什么用这个符号表示呢？其实，这个符号是拉丁文r的变形，在拉丁文中，r是“根”的首字母。16世纪时，人们表示根号用的是大写的拉丁字母R，并且会在它的后面加上“平方”的首字母“q”，或者“立方”的首字母“c”，以此表示开几次方，比如

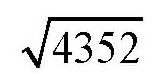
那时候的写法是

R.q.4352

此外，那时候的加号和减号也跟现在不一样，而是分别用字母p和m表示；括号则是用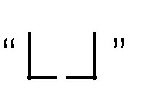

表示。所以，对于我们来说，那时候的代数公式看起来会很不习惯。

下面这个式子出现在古代数学家邦别利的：

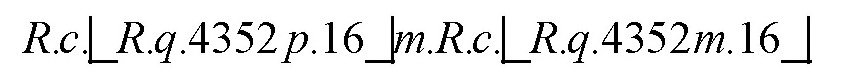
将它翻译为现在的代数语言，即

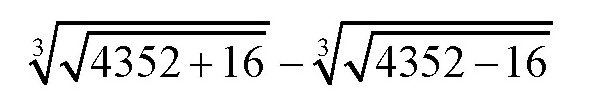
对于

，我们还可以把它表示成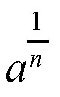

，这个符号是由16世纪荷兰的著名数学家斯台文提出的。这种表示方法有利于概括问题，即可以把方根看成是乘方，只不过这时候的指数为分数罢了。