在实地测量一个角度的时候,通常只需要一个指南针或者几根手指或者火柴盒就可以了。但是,有时候,我们会遇到这样的情形:不是让我们实地测量,而是要测量出画在纸上、平面图上或者地图上的角的大小。
当然,如果我们的手头有一个量角器,问题就很容易解决了。但是,如果没有量角器,我们该怎么测量呢?在这种情况下,利用几何学的知识,也是可以解决的。下面,我们就来举一个例子。
【题目】如图所示,∠AOB是一个小于180°的角,如果不作任何测量,你可以求出这个角的大小吗?
【解答】如果根据前面的方法,我们可以从BO上的任一点作垂直于AO的垂线,测量出直角三角形每个边的长度,然后算出这个角的正弦值,根据正弦值得出这个角的大小。但是,题目的要求是不作任何测量。所以,我们需要另找方法。这时,我们可以这样做:
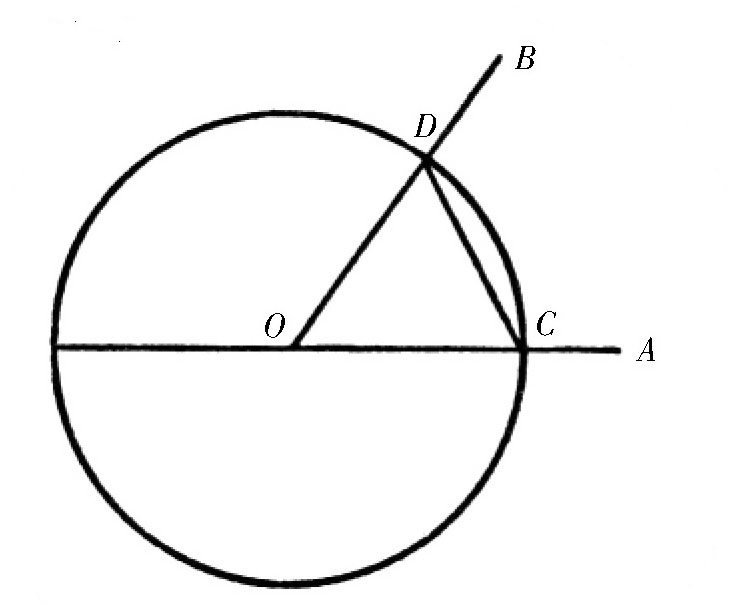
图 只使用圆规,求出∠AOB的大小。
以∠AOB的顶点O为圆心,任意长度为半径,作一个圆。圆周跟AO、BO分别相交于点C、D,连接CD。
然后,拿一个圆规,从点C开始,按照CD的长度,在圆周上沿同一个方向一直量下去,直到圆规的一个脚再次落到点C为止,记住测量的次数,也就是一共测量了多少段,以及圆规绕圆周的次数。
假设圆规在这个圆周上测量了S段CD的长度,并且绕圆周的次数是n。那么,∠AOB的大小就是:
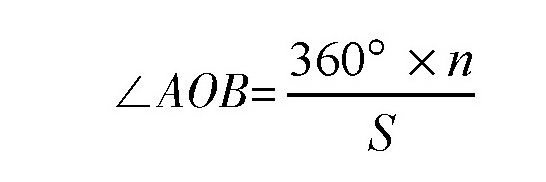
这是为什么呢?其实,我们可以这样分析:假定这个角是x,如果圆规在圆周上测量了S次,就相当于把x的角扩大到S倍,同时,圆周被绕了n次,就相当于这个角等于360°×n,所以:
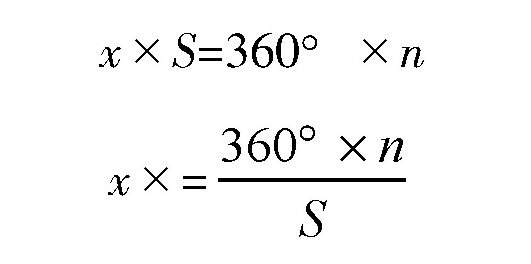
在图中,用圆规测量的结果是n=3,S=20,所以∠AOB=54°。
如果没有圆规,我们还可以用一个大头针或者一张纸条来测量。
【思考题】利用图的方法,求出图中各个角的大小。
