假设水路的运费是公路的一半,现在想在点D处修一条公路通往点B,使得从城市A到点B的运费最少,那么,点D应该选在什么地方?

【题目】如图所示，有一批货物要从河边的城市A运到下游方向的点B处，已知点B在河下游a千米的地方，并且距离河岸d千米。假设水路的运费是公路的一半，现在想在点D处修一条公路通往点B，使得从城市A到点B的运费最少。那么，点D应该选在什么地方？

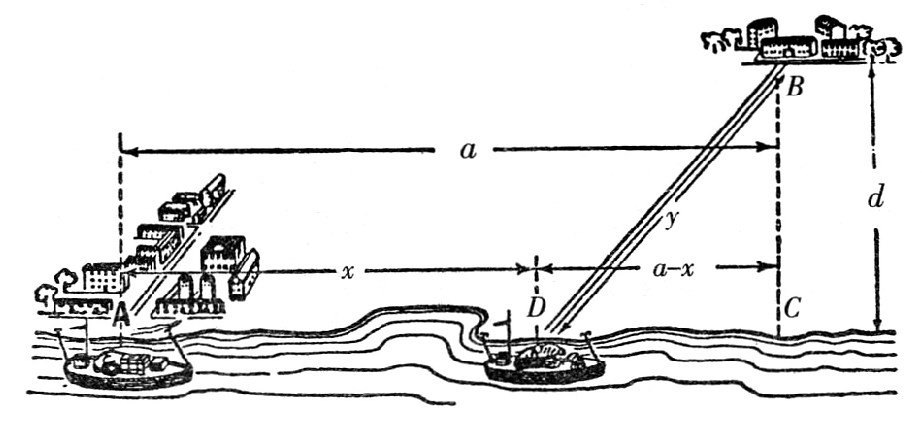
【解答】设距离AD=x，公路的长度BD=y。由题意知，AC=a，BC=d。公路的运费是水路的2倍，要求总的运费最小就相当于求

x+2y

的最小值。

由已知得，x=aDC，而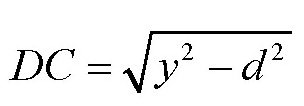

。设x+2y=m，则有

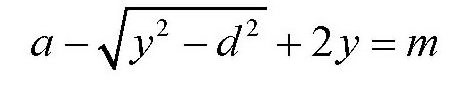
去根号，得

3y²-4(m-a)y+(m-a)²+d²=0

解方程得

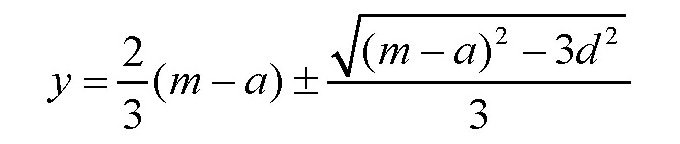
由于y必为实数，所以(m-a)²≥3d²。因此(m-a)²的最小值为3d²，这时

在图中，

。即

所以，∠BDC＝60°。也就是说，不论a多长，只要使公路与河的夹角为60°就可以了。

在这个题目中，我们遇到了跟前面一样的情况，方程的解只在某些条件下才有意义。如果城市A和点B的连线与河的夹角为60°，则根本不需要水路运输，直接在城市A和点B之间修一条公路就可以了。