一块矩形铁片把它做成一个截面为等腰梯形的槽,应该如何做这个槽才能使它的截面积最大?

【题目】如图所示，这是一块矩形铁片，现在想把它做成一个截面为等腰梯形的槽。

从图和图可以看出，这种槽的样子很多。请问，应该如何做这个槽，才能使它的截面积最大？

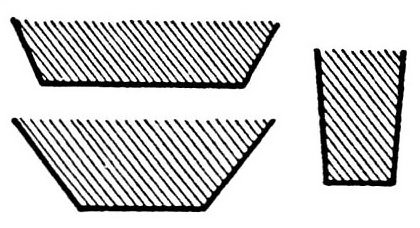
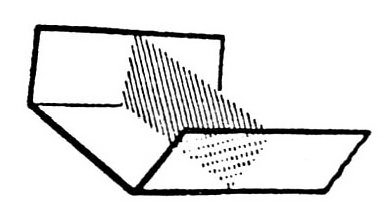
【解答】设铁片的宽度为l，槽侧面的宽度为x（即截面等腰梯形的腰长为x），底面的宽度y，并引入未知数z来表示如图所示的部分。

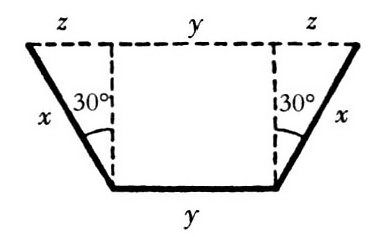
槽的截面为梯形，该面积为

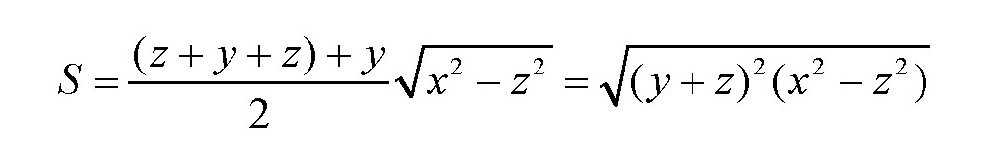
现在的问题就是求出x，y和z的值，使面积S最大。另外，这里的2x+y=l为定值。

对上面的等式进行变换，得

S²=(y+z)²(x+z)(x-z)

等式两边同乘以3，得

3S²=(y+z)3S(x+z)(3x-3z)。

从上式可以看出，右边的4个乘数之和为

(y+z)+(y+z)+(x+z)+(3x-3z)=2y+4x=2l

即为定值。根据之前的结论，当这4个乘数相等时，它们的乘积最大。即

y+z=x+z

y+z=3x-3z

容易得出

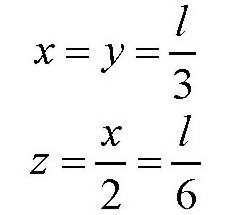
由图可以看出，在两个三角形中，直角边z为斜边x的一半，所以直角边z对应的角为30°，从而梯形的腰跟底边的夹角为120°。

也就是说，当槽的截面正好是正六边形的3个相邻边时，这个槽的截面积最大。