在Chapter1中我们提到,代数的第五种运算有两种逆运算:一种是开方,另一种是取对数。比如:
ab=c
如果求a就是开方,而求b就是取对数。如果你学习过中学数学课本中的内容,那么对于下面的表达式
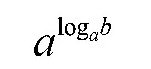
你应该可以理解它的意思,并求出它的值。
容易理解,如果把上面的底数a进行乘方,而且这个乘方的次数是以a为底b的对数,那么,结果正好等于b。
你知道为什么发明对数吗?毫无疑问,就是为了使运算更加方便。对数是由耐普尔发明的,他曾这样说过:
“我要尽最大的努力,降低运算难度,减少运算量,很多人就是因为数学运算太复杂而对数学产生了恐惧。”
实际上,对数确实可以简化运算。甚至在有的情况下,离开了对数,运算根本无法进行,比如对任意指数进行开方。
数学家拉普拉斯也说过:“对数的出现,使原来几个月才能完成的运算,只需要几天就能完成。毫不夸张地说,对数的引入,让天文学家的寿命成倍延长。”因为天文学家经常需要进行非常复杂的运算。事实上,对于所有的领域,只要跟数学打交道,对数都可以简化运算,这是不争的事实。
如今我们已经可以熟练地运用对数,并把它对运算的简化看作很平常的事情。很难想象,在它刚被发明的时候,人们该有多么惊叹它的巨大威力。
与耐普尔同时代的布利格,发明了常用对数。他在读了耐普尔的著作后,说:“耐普尔发明的对数太新颖、太奇妙了,我想尽快见到耐普尔本人,我从来没有读过让我如此喜欢、如此惊叹的书。”后来,他真的在苏格兰见到了耐普尔。据说他见到耐普尔后,是这么说的:
“我不远万里到这里来的唯一目的,就是想拜见您。我很想知道,您到底拥有怎样的聪明才智,才发明了这个妙不可言的工具——对数?而且,我非常不明白的是,为什么以前的人没有想到,但是当你发明了以后,它看起来又是如此简单!”
