【题目】在一块三角形的硬纸板上切出一个面积最大的矩形,并且要求矩形的边跟三角形的底和高平行。
【解答】如 图 所示,假设硬纸板的形状是三角形ABC,图形MNOP就是我们要切出的那个矩形。根据题意我们可以得到,三角形ABC和三角形MBN是相似三角形,所以:


图 三角形中的内接矩形的面积。
假设矩形其中一条边的长度为y,三角形顶点B到线段MN的距离BE为x,三角形的底边AC的长度为a,三角形的高BD的长度为h,则上式可以写为:
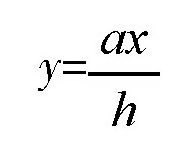
所以,矩形MNOP的面积S为:

所以:

根据题意,h和a都是定值,所以当)h-x)x取得最大值的时候,面积S最大。而右边式子中的两个乘数h-x与x之和为定值h,所以右边式子将在这两个乘数相等的时候取得最大值,即:
h-x=x
所以:

矩形的边MN的长度应该等于三角形的高的一半,它会通过高的中点。因此只要找到三角形两个边的中点,并连接它们,就得到了这个矩形的一条边,它的长度为
,另一条边的长度为
