有一段圆木,现在想锯出一条方木梁,要求它的质量越重越好,那么,我们该怎么锯呢?

【题目】我们有一段圆木，现在想锯出一条方木梁，要求它的质量越重越好。那么，我们该怎么锯呢？

【解答】分析题意，我们可以把这个题目转化为这样一个问题：在一个已知圆中，如何画出一个面积最大的矩形。在学习了前面的内容后，读者朋友可能已经有了答案，这个矩形必须是正方形。下面，我们就来证明一下这个结论，其实，这个过程还是很有意思的。

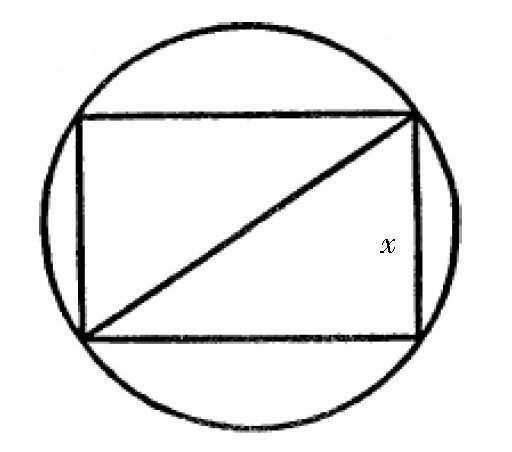
图 质量最大的方木梁。

如 图 所示，矩形其中一个边的长度用x表示，那么另一个边的长度就是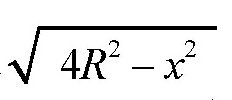

，这里的R为圆木的半径。所以矩形的面积就是：

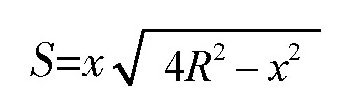
两边平方，得到：

S²=x²)4R－x²)

在上式中，右边的两个乘数x²与4R²-x²之和是一个定值4R²，所以它们的乘积x²)4R²-x²)，也就是S²在乘数x²与)4R²-x²)相等的时候最大。它们相等时面积S的值，就是所求的最大面积。

也就是说，当这个矩形是正方形的时候，它的面积最大。这时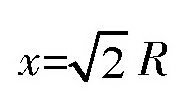

。实际上，这个正方形为圆的内接正方形。

综上所述，如果把这段圆木的截面锯成正方形，这时木梁的体积最大，质量也最重。