现在,就连一个初中生都知道利用直径来计算圆周的长度。但是,在古时候,即使是埃及的祭司或者罗马帝国最杰出的建筑师也很难精确计算出圆周的长度来。那时候,埃及人认为圆周的长度是直径的3.16倍,罗马人则认为这个倍数是3.12。现在,我们知道了,这个倍数其实是3.14159……当时,那些数学家并不像后来的数学家那样,利用几何学知识进行计算,他们是根据经验来计算的。那么,为什么会产生这么大的误差呢?很简单就可以得到这个比例关系!只要用一根丝线绕在一个圆的东西上,然后测量出它的长度,以及这个圆东西的直径,不就得出来了吗?
其实,他们就是这么做的。你可能以为这很简单,但是你知道这样做得到的结果并不一定很准确吗?我们知道,如果一个圆瓶的直径是100毫米,那圆周的长度就应该是314毫米。但是,在用细线测量的时候,并不一定能得到这样的结果。1毫米的误差已经很小了。如果真的是1毫米的误差,那算出来的π的值就是3.13或者3.15。而且,还有一点,测量圆瓶的直径时,也不一定测量得非常精确,也有可能产生1毫米的误差。那么这个π值就会介于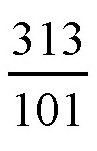
和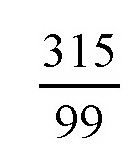
之间,如果表示成小数,就是3.09~3.18。
从这里可以看出,通过这种方法来得到的π值跟3.14相比,误差是比较大的,可能是3.1、3.12,或者3.17。当然了,也有可能正好碰上3.14,但是,跟其他的值一样,这个值并没有让测量的人觉得有什么特别的意义。
通过这样的实验,根本不可能得出可以使用的π值。说到这里,我们就清楚了,古时候的人为什么得不到圆周长度跟直径的确切比值了。而阿基米德是通过思考,才得到了π值: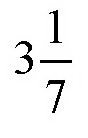
。
