3个相同的数字排列的秘密,不使用运算符号用3个相同的数摆出一个尽可能大的数

通过前面的几个例子，读者可能会产生这样的困惑：为什么有些数字用三层的摆法最大，而有些数字就不是呢？下面，我们就来深入讨论一下这个问题，先来看一般的情形。

不使用运算符号，用3个相同的数摆出一个尽可能大的数。用字母a表示一个数，下面的摆法：示一个数，下面的摆法：

2²²，3³³，4⁴⁴

就可以表示为

a^10a+a＝a^11a

a的三级“超乘方”则可以表示为

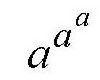
问题的关键在于，当a取何值时，用三层摆法得到的数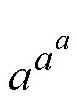

比a^11a大。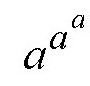

与a^11a是以同一个数作为底的乘方，由于又都是整数，所以只需要比较它们指数的大小就可以了，指数大的，得到的数就大。上面的问题归结为求解下面的不等式：

a^a＞11a

不等式两端都除以a，可以得出：

a^a-1＞11

通过代入法，我们可以得到，当a＞3时，a^a-1＞11成立。例如，当a=4时，

4^4-1＞11

显然是成立的，而3^3－1，2^2－1都比11要小。

由此，得出结论：当这个数为2或者3的时候，用a^11a的形式摆出的数最大；而当这个数大于等于4时，用三层摆法得到的数最大。